初めに言っておくと
Rならt分布とかX^2分布に従う乱数とかすぐにできるんだけど、あえてそれを正規乱数から生成してみるというやつです。X^2分布
wikipedia:カイ二乗分布より引用すると「なので、ここでは標準正規乱数の和を用いてX^2分布に従う乱数を生成してみましょう。以下では標準正規乱数を1000個作っています。
rnorm(1000,0,1)
標準正規乱数の和がX^2分布に従う乱数ということなので、以下の操作で自由度1000のX^2分布に従う乱数が一つ生成できました*1。やったね!!
> sum(rnorm(1000,0,1)) [1] -40.39547
しかし、乱数が一つできただけではうれしくないので、いくつか作りましょう。
sapply(1:100,function(x){sum(rnorm(1000,0,1))})
"function(x)"となっていますが、xを書かないとRに怒られるからというだけの理由です。
さて、これでX^2分布に従う乱数が本当にできたのでしょうか?id:syou6162の言うことはうのみにできませんね。
冒頭に述べたようにRではかなりの種類の乱数を生成できて*2、X^2分布に従う乱数ももちろん生成できます。以下のようにやると自由度1000のX^2な乱数が100個生成されます。
> rchisq(n=100,df=1000) [1] 1004.8246 1037.5194 1102.4398 974.8221 987.7748 957.7497 1014.5186 [8] 1009.8056 985.1967 1006.9750 925.1211 951.8096 1033.2675 933.1105 [15] 986.2319 944.5343 956.8831 995.8095 1000.8527 1045.7485 1015.2639 [22] 1021.2010 1028.5797 992.2410 1060.9658 992.5542 992.1579 1108.8188 [29] 948.9250 1025.6664 949.1166 985.6636 1081.2387 993.1824 1044.0235 [36] 990.5063 970.1770 1040.4290 972.9672 1020.0634 938.4145 922.3377 [43] 1012.6435 1016.1597 1004.4085 1049.0279 961.8093 1061.1697 971.9376 [50] 1086.0452 994.4034 987.8005 1080.3712 1061.5354 1044.8115 939.4044 [57] 960.9035 1086.2686 990.2781 985.0040 1036.0976 1036.1089 953.1455 [64] 971.9200 919.7944 989.3699 966.1771 995.5862 1065.4485 1031.2868 [71] 1083.8010 908.1108 936.5850 996.6828 950.7488 978.2935 908.4841 [78] 1017.5772 948.6313 1058.0582 1031.7838 971.6462 1029.0020 978.3422 [85] 1082.2388 1093.5395 1003.8404 1034.2276 1032.2080 986.0336 975.6113 [92] 1045.7243 1001.7460 941.9326 1027.8468 1003.7567 979.5090 966.3077 [99] 942.1988 1015.8021
二つのデータ列が同一の分布をしている、ということはどうやって調べるのでしょうか?それはqqplotというものを使うと分かります。qqplotについてはこの辺に書いてますし、Tsukuba.Rの発表でも少し登場しています。このqqplotを前の二つのデータに対して使ってやると、下のような図ができます。
qqplot(sapply(1:100,function(x){sum(rnorm(1000,0,1))}),rchisq(n=100,df=1000))
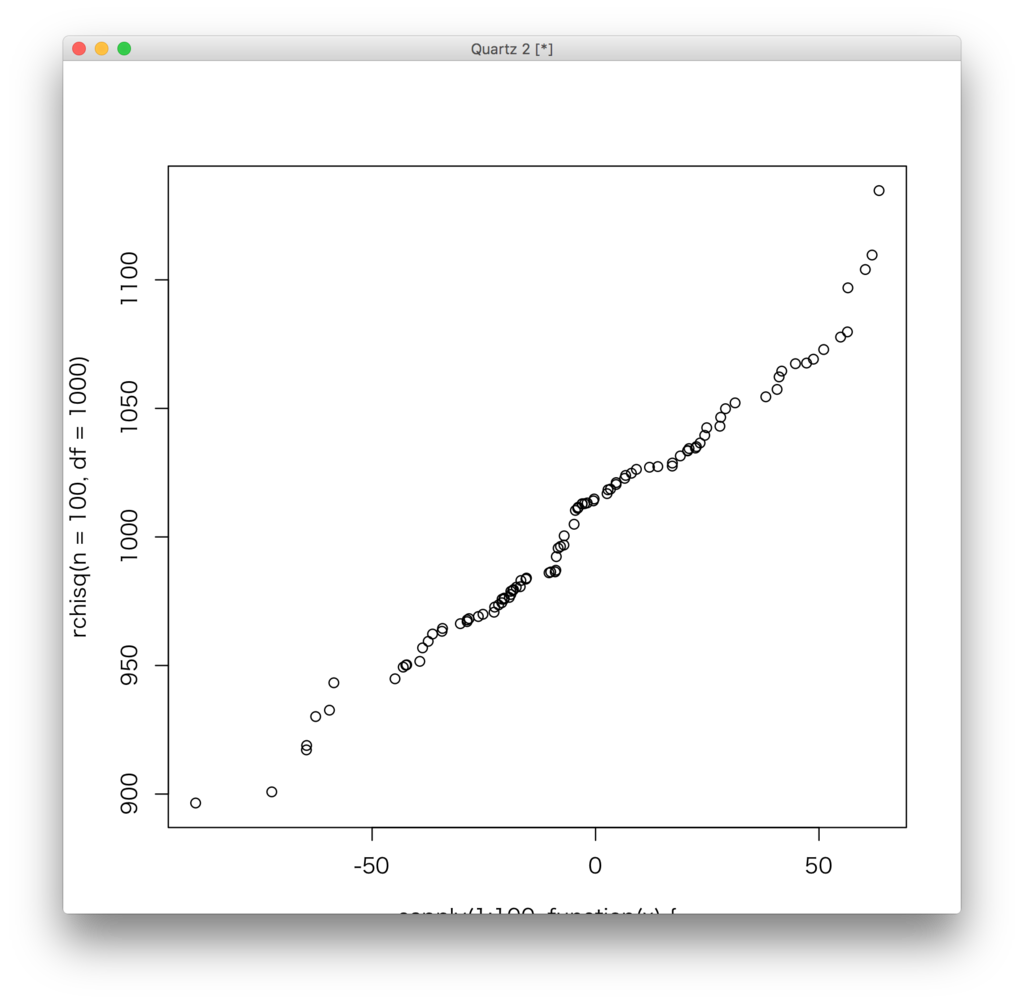
ほぼ直線に従っている、と見なすことができるので、id:syou6162が作ったX^2分布に従う乱数でありそうだということが確認できました。
X^2分布って何の役に立つの?おいしいの?
X^2分布は独立性の検定というのによく使われます。詳しくは下のような感じです。
アンケートとかを取ったらクロス表みたいなのを作るのがよくあるんですが、例えば「男と女で回答結果に差があるか?」のようなものを確かめたい!!という時にX^2分布というのは利用されます。
t分布
これまたwikipediaより引用。t分布は平均の差の検定とかでよく出てくるので割りと知られているのかもしれません。「が、平均
、分散
の正規分布に従う独立でランダムな変数であるとする。 また標本平均を
とし、不偏分散を
とする。ここで次の変数
を考えると、これは
(ただし
、
はガンマ関数という確率密度関数に従うことが、ゴセットによって示された。ここでTの従う分布をt分布(またはスチューデント分布)と呼ぶ。」とあります。
なんか見たくもない数式が出てきました、僕もこんなの覚えてないので、まあいいです。正規分布からなる確率変数の標本平均に基準化のようなものをするとt分布に従うような乱数ができる、と書いてあるわけです。「基準化のような」というのは不偏分散で割っているところからきています。
「不偏分散とか書いてあるけど、他にも分散ってあるのかよ」とか言いたくなりますが、あります。標本分散と呼ばれるもので、のように計算されるものです。標本分散は分散を過少評価していて、あまりよいものではありません。特に少標本*3の時だと問題になってきます。そういうわけで、不偏分散がよく使われます。Rで分散を計算するvar関数も不偏分散の式で計算されていた、はずです。
不偏分散の付近はもっと正確に言うならば、不偏分散は期待値が真の分散の値に一致する(このようなものを不偏推定量と呼びます)、ということなのですが、この辺を知りたい人はwikipedia:分散の付近とかおってみるといいんじゃないかと思います。
まあ、不偏分散の説明はこの辺にして。「正規分布からなる確率変数の標本平均に基準化のようなものをするとt分布に従うような乱数ができる」ということでした。というわけなので、X^2の時のように自前乱数とRでのt分布に従う乱数を比較してみます。
n <- 6 df <- n-1 myrt <- function(){ mu <- 5 sigma <- 3 x <- rnorm(n,mu,sigma) y <- sum(x)/n (y - mu) / sqrt((var(x)/n)) } sample.number <- 10000 myrt.sample <- sapply(c(1:sample.number),function(x){myrt()}) rt.sample <- rt(sample.number,df) qqplot(rt.sample,myrt.sample)
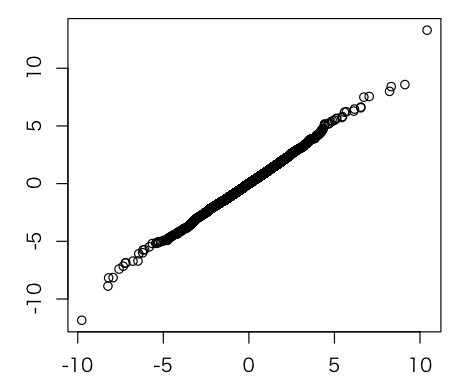
これも直線になっていて、よさそうですね!!なんかいかやると「これ直線に従うっていっていいのかな?」という例に出会うかもしれませんが、系統的にはずれていなければ大丈夫です。
ところで、t分布はnが小さいとき*4、t分布と正規分布はあまり似ていません。実際にやってみると下のようになります。系統的に直線に従っていないので、分布が異なると言えそうです。
n <- 6 df <- n-1 myrt <- function(){ mu <- 5 sigma <- 3 x <- rnorm(n,mu,sigma) y <- sum(x)/n (y - mu) / sqrt((var(x)/n)) } sample.number <- 10000 myrt.sample <- sapply(c(1:sample.number),function(x){myrt()}) rnorm.sample <- rnorm(sample.number,0,1) qqplot(rnorm.sample,myrt.sample)
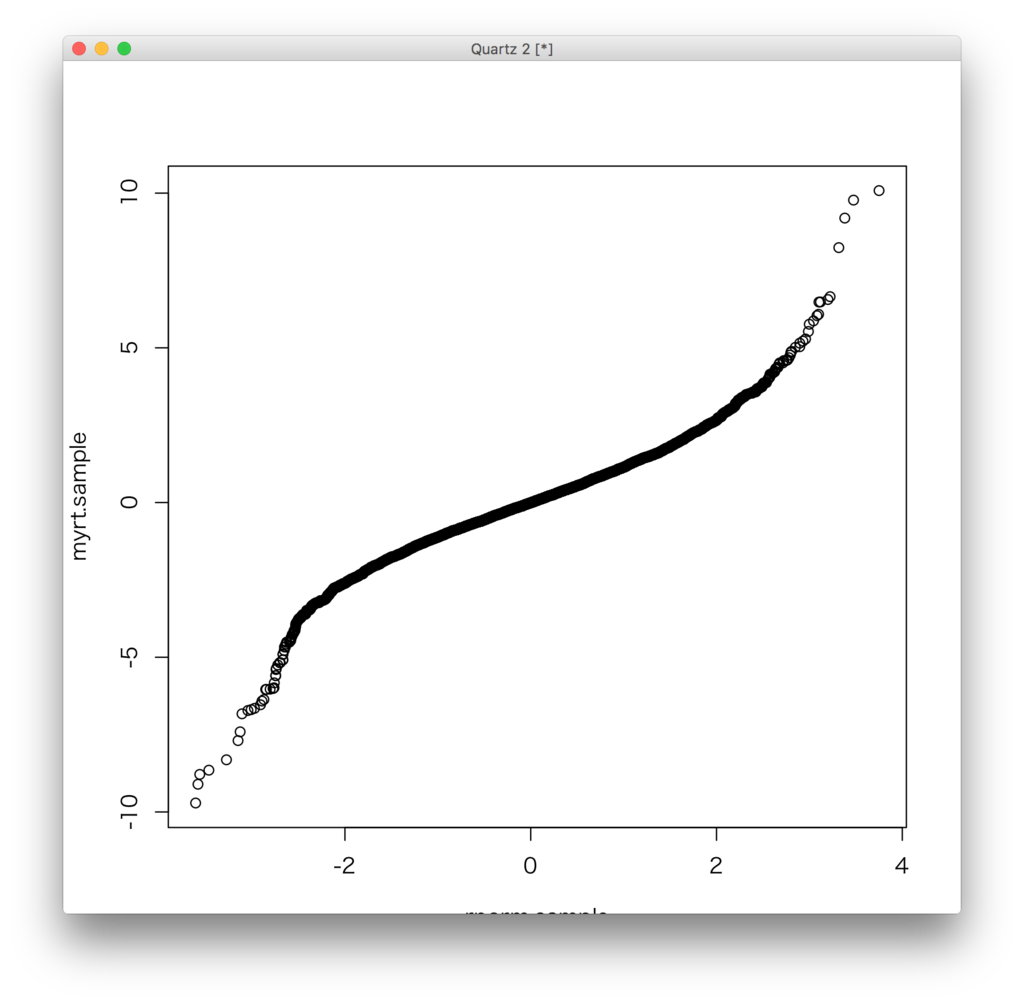
しかし、nを増やしていくにつれて、t分布は正規分布に近づいていきます。下のqqplotがほぼ直線になっていることからも確認できます。
n <- 1000 df <- n-1 myrt <- function(){ mu <- 5 sigma <- 3 x <- rnorm(n,mu,sigma) y <- sum(x)/n (y - mu) / sqrt((var(x)/n)) } sample.number <- 10000 myrt.sample <- sapply(c(1:sample.number),function(x){myrt()}) rnorm.sample <- rnorm(sample.number,0,1) qqplot(rnorm.sample,myrt.sample)
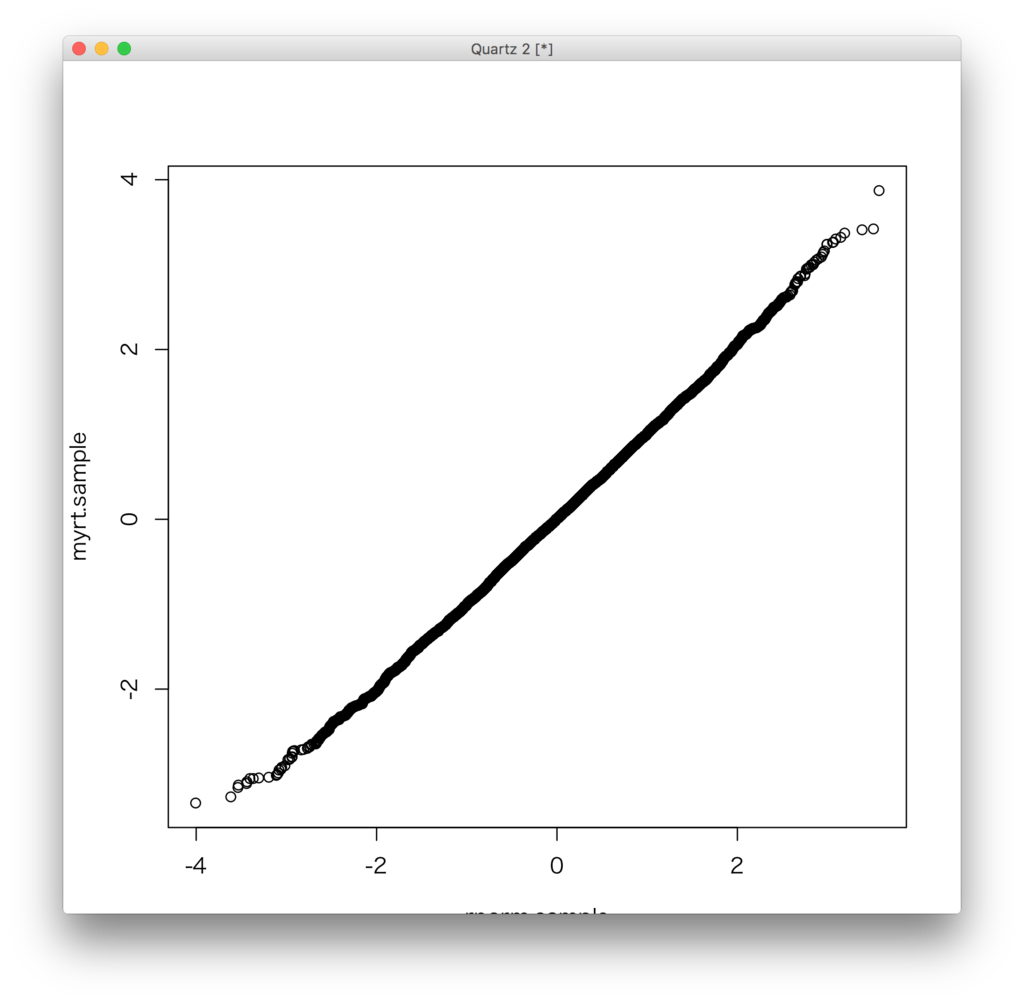
解析的にも「自由度の値を大きくするとt分布は標準正規分布に近づく」ということが証明されています。面白いですね。

数学ガールの秘密ノート/やさしい統計 (数学ガールの秘密ノートシリーズ)
- 作者: 結城浩
- 出版社/メーカー: SBクリエイティブ
- 発売日: 2016/10/29
- メディア: 単行本
- この商品を含むブログ (12件) を見る
*1:1000に特に意味はありません
*2:http://www.okada.jp.org/RWiki/index.php?%CD%F0%BF%F4Tips%C2%E7%C1%B4を参照すればよい
*3:サンプル数が少ない、ということ
*4:自由度が小さい、ということ