解禁します

最終レポートの提出期限も過ぎたのでレポートで使ったRのコードを公開します。内容としてはこの辺でも触れた回帰モデルのパラメータの分布の話について。

誤差項が平均0で有限の分散を持つならば、中心極限定理を使えるくらいNが大きければ誤差項の分布は正規分布ではなくても問題はない。条件を満たしているならば、パラメータは漸近的に正規分布に近づき、t検定なども行える。

すっきりした - Seeking for my unique color.

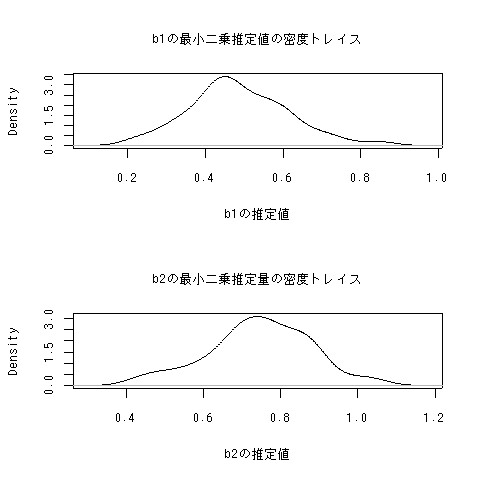
誤差項が正規分布をする場合。パラメータも正規分布してます。

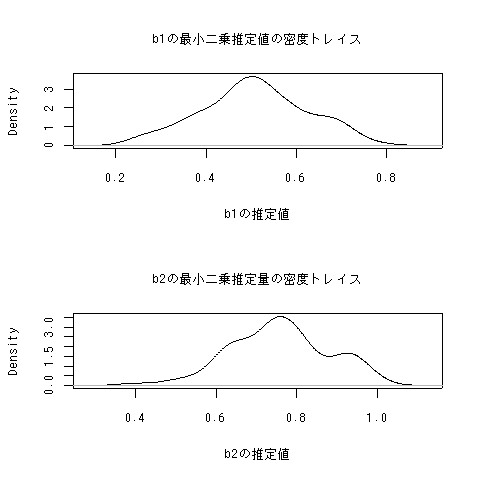
誤差項が一様分布の場合。Nを大きくすると中心極限定理が使えるので、パラメータの分布としては正規分布に漸近的に近付きます。実際の分布もそんな感じ。

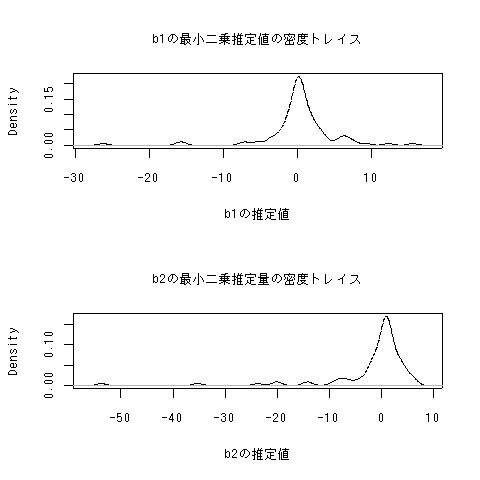
誤差項がコーシー分布に従う場合、誤差項は有限の積率を持たないので中心極限定理を使うことができず、パラメータの分布も正規分布から離れたものになってしまう。実際のやつもすっごいぶっとんでいることが分かりますね。

ちなみに誤差項がランダムウォークしてしまう場合は、Nを大きくするにつれてパラメータの分散も無限大に発散してしまうので推定値として使いものになりません。

あとはコードだよ。何かかなり長いのは気のせいwww。

#計量時系列分析の課題
getwd()
setwd("~/Desktop/work/ts/img/")

x11 <- rnorm(1)*0.5
x1 <- c()
x1[1] <- x11
for(i in 1:199){
  x1[i+1] <- 0.6*x1[i]+rnorm(1)*0.5
}

png("ts.plot.x1.png")
plot(x1,type="l",main="N=200のときのx1の時系列プロット")
dev.off()

png("acf.x1.png")
acf(x1,main="N=200のときのx1の標本自己相関係数")
dev.off()

png("pacf.x1.png")
pacf(x1,main="N=200のときのx1の標本偏自己相関係数")
dev.off()

x21 <- rnorm(1)*0.5
x2 <- c()
x2[1] <- x21
e.old <- rnorm(1)*0.5
for(i in 1:199){
  e.new <- rnorm(1)*0.5
  x2[i+1] <- e.new-0.4*e.old
  e.old <- e.new
}

png("ts.plot.x2.png")
plot(x2,type="l",main="N=200のときのx2の時系列プロット")
dev.off()

png("acf.x2.png")
acf(x2,main="N=200のときのx2の標本自己相関係数")
dev.off()

png("pacf.x2.png")
pacf(x2,main="N=200のときのx2の標本偏自己相関係数")
dev.off()

mu <- rnorm(200)
y <- 0.5*x1+0.75*x2+mu

hist(y)
plot(y)

summary(lm(y~-1+x1+x2))

#面倒だから関数にしちゃう
make.x1 <- function(n){
  x11 <- rnorm(1)*0.5
  x1 <- c()
  x1[1] <- x11
  for(i in 1:(n-1)){
    x1[i+1] <- 0.6*x1[i]+rnorm(1)*0.5
  }
  return(x1)
}

make.x2 <- function(n){
  x21 <- rnorm(1)*0.5
  x2 <- c()
  x2[1] <- x21
  e.old <- rnorm(1)*0.5
  for(i in 1:(n-1)){
    e.new <- rnorm(1)*0.5
    x2[i+1] <- e.new-0.4*e.old
    e.old <- e.new
  }
  return(x2)
}

make.y <- function(x1,x2,n){
  mu <- rnorm(n)
  y <- 0.5*x1+0.75*x2+mu
  return(y)
}

n <- 200
x1 <- make.x1(n)
x2 <- make.x2(n)

for(i in 1:100){
  y <- make.y(x1,x2)
  mat[i,] <- lm(y~-1+x1+x2)$coef
}

make.par <- function(x1,x2,n){
  mat <- matrix(0,100,2,byrow=T)
  for(i in 1:100){
    y <- make.y(x1,x2,n)
    mat[i,] <- lm(y~-1+x1+x2)$coef
  }
  return(mat)
}  

hist(make.par(x1,x2,200)[,2])

my.summary <- function(x){
  mu <- mean(x)
  var <- var(x)
  return(list(mu=mu,var=var))
}

make.hist <- function(mat){
  par(mfrow=c(2,1))
  hist(mat[,1],main="b1の最小二乗推定値のヒストグラム",xlab="b1の推定値")
  hist(mat[,2],main="b2の最小二乗推定値のヒストグラム",xlab="b2の推定値")
}

make.density <- function(mat){
  par(mfrow=c(2,1))
  plot(density(mat[,1]),main="b1の最小二乗推定値の密度トレイス",xlab="b1の推定値")
  plot(density(mat[,2]),main="b2の最小二乗推定量の密度トレイス",xlab="b2の推定値")
}

mat <- make.par(x1,x2,200)
png("hist.par.png")
make.hist(mat)
dev.off()

png("density.par.png")
make.density(mat)
dev.off()

my.summary(mat[,1])
my.summary(mat[,2])
my.summary(make.par(100)[,1])
my.summary(make.par(50)[,1])
my.summary(make.par(25)[,1])

make.y.for.uni <- function(x1,x2,n){
  mu <- (runif(n)-1/2)*2*sqrt(3)
  y <- 0.5*x1+0.75*x2+mu
  return(y)
}

1/sum(x1^2)
1/sum(x2^2)
mat
t(mat)%*%mat
solve(t(cbind(x1,x2))%*%cbind(x1,x2))

hist((runif(100)-1/2)*2*sqrt(3))

make.par.for.uni <- function(x1,x2,n){
  mat <- matrix(0,100,2,byrow=T)
  for(i in 1:100){
    y <- make.y.for.uni(x1,x2,n)
    mat[i,] <- lm(y~-1+x1+x2)$coef
  }
  return(mat)
}  

n <- 200
x1 <- make.x1(n)
x2 <- make.x2(n)
make.par.for.uni(x1,x2,n)

my.summary(make.par.for.uni(200)[,1])
my.summary(make.par.for.uni(100)[,1])
my.summary(make.par.for.uni(50)[,1])
my.summary(make.par.for.uni(25)[,1])

n <- 1000
my.summary(sqrt(n)*(0.5-make.par.for.uni(n)[,1]))

plot(density(sqrt(n)*(0.5-make.par.for.uni(n)[,1])))

plot(density(rnorm(1000000)))

sum(x1^2)
sqrt(200)
sum(x1^2)

n <- 200
my.value <- c()
for(i in 1:20){
  my.value[i] <- my.summary(sqrt(n)*(make.par.for.uni(n)[,1]-0.5))$var
}
my.summary(my.value)

n <- 200
my.value <- c()
for(i in 1:20){
  my.value[i] <- my.summary(sqrt(n)*(make.par(n)[,1]-0.5))$var
}
my.value
mean(my.value)

sqrt(n)*(make.par.for.uni(n)[,1]-0.5)

n <- 10000

x1 <- make.x1(n)
x1

x2 <- meke.x2(n)
plot(density(x1/(n/sum(x1^2))))
mean(x1)
var(sqrt(n)*(make.par.for.uni(n)[,1])-0.5*sqrt(sum(x1^2)))

var(0.5/(1/sum(x1^2)))

#x1,x2は使いまわさないといけないことを忘れていた。その辺を考慮した上でファンクションをもう一回作りなおさないといけない
#パラメータの分散の平均値は大体いい感じになった

x1

hist(sqrt(200)*(0.5-make.par.for.uni(200)[,1]))
my.summary(sqrt(200)*(0.5-make.par.for.uni(200)[,1]))

my.summary(rnorm(2000))

sum(x1^2)

dim(x1)
x2 <- make.x2(n)
x2
solve(t(cbind(x1,x2))%*%cbind(x1,x2))
#結局sumした値と変わらない

#こっちが理論値。ほとんど0に近い値になっちゃった。
1/(sum(x1^2))
10000/(sum(x1^2))

sqrt(10009)

my.value <- c()
for(i in 1:20){
  n <- 2000
  x1 <- make.x1(n)
  x2 <- make.x2(n)
  my.value[i] <- n/(sum(x1^2))
}

my.summary(my.value)

n <- 2000
x1 <- make.x1(n)
x2 <- make.x2(n)
y <- make.y.for.uni(x1,x2,n)
hist(y)
summary(lm(y~-1+x1+x2))

#n=25
n <- 25
x1 <- make.x1(n)
x2 <- make.x2(n)
mat <- make.par(x1,x2,n)
png("hist.par25.png")
make.hist(mat)
dev.off()
png("density.par25.png")
make.density(mat)
dev.off()

my.summary(mat[,1])
my.summary(mat[,2])

solve(t(cbind(x1,x2))%*%cbind(x1,x2))

#n=50
n <- 50
x1 <- make.x1(n)
x2 <- make.x2(n)
mat <- make.par(x1,x2,n)
png("hist.par50.png")
make.hist(mat)
dev.off()
png("density.par50.png")
make.density(mat)
dev.off()

my.summary(mat[,1])
my.summary(mat[,2])

solve(t(cbind(x1,x2))%*%cbind(x1,x2))

#n=100
n <- 100
x1 <- make.x1(n)
x2 <- make.x2(n)
mat <- make.par(x1,x2,n)
png("hist.par100.png")
make.hist(mat)
dev.off()
png("density.par100.png")
make.density(mat)
dev.off()

my.summary(mat[,1])
my.summary(mat[,2])

solve(t(cbind(x1,x2))%*%cbind(x1,x2))

#一様分布
n <- 200
x1 <- make.x1(n)
x2 <- make.x2(n)
mat <- make.par.for.uni(x1,x2,n)
png("hist.par.for.uni25.png")
make.hist(mat)
dev.off()
png("density.par.for.uni25.png")
make.density(mat)
dev.off()

my.summary(mat[,1])
my.summary(mat[,2])

solve(t(cbind(x1,x2))%*%cbind(x1,x2))

#一様分布

n <- 25
x1 <- make.x1(n)
x2 <- make.x2(n)
mat <- make.par.for.uni(x1,x2,n)

png("hist.par.for.uni25.png")
make.hist(mat)
dev.off()
png("density.par.for.uni25.png")
make.density(mat)
dev.off()

my.summary(mat[,1])
my.summary(mat[,2])

solve(t(cbind(x1,x2))%*%cbind(x1,x2))

n <- 50
x1 <- make.x1(n)
x2 <- make.x2(n)
mat <- make.par.for.uni(x1,x2,n)

png("hist.par.for.uni50.png")
make.hist(mat)
dev.off()
png("density.par.for.uni50.png")
make.density(mat)
dev.off()

my.summary(mat[,1])
my.summary(mat[,2])

solve(t(cbind(x1,x2))%*%cbind(x1,x2))


n <- 100
x1 <- make.x1(n)
x2 <- make.x2(n)
mat <- make.par.for.uni(x1,x2,n)

png("hist.par.for.uni100.png")
make.hist(mat)
dev.off()
png("density.par.for.uni100.png")
make.density(mat)
dev.off()

my.summary(mat[,1])
my.summary(mat[,2])

solve(t(cbind(x1,x2))%*%cbind(x1,x2))

n <- 200
x1 <- make.x1(n)
x2 <- make.x2(n)
mat <- make.par.for.uni(x1,x2,n)

png("hist.par.for.uni200.png")
make.hist(mat)
dev.off()
png("density.par.for.uni200.png")
make.density(mat)
dev.off()

my.summary(mat[,1])
my.summary(mat[,2])

solve(t(cbind(x1,x2))%*%cbind(x1,x2))

png("uniform.qq.png")
par(mfrow=c(2,1))
par(oma=c(0,0,3,0))
qqnorm(mat[,1],main="b1のQ-Qプロット")
qqline(mat[,1])
qqnorm(mat[,2],main="b2のQ-Qプロット")
qqline(mat[,2])
mtext(side=3,outer=TRUE,text="b1、b2の最小二乗推定値のQ-Qプロット")
dev.off()

plot(density(rnorm(100)))

n <- 200
x1 <- make.x1(n)
x2 <- make.x2(n)
y <- make.y.for.uni(x1,x2,n)
summary(lm(y~-1+x1+x2))
mat <- make.par.for.uni(x1,x2,n)

make.density(scale(mat))
hist(0.5-mat[,1])
rbinom(10,100,0.2)
plot(density(0.5-mat[,1]))
my.summary(mat[,2])
qqnorm(mat[,1])
qqline(mat[,1])
png("density.par.for.uni200.png")
make.density(mat)
dev.off()
my.summary(mat[,1])
my.summary(mat[,2])

n <- 200
x1 <- make.x1(n)
x2 <- make.x2(n)
var(sqrt(n)*(0.75-make.par.for.uni(x1,x2,n)[,2]))
y.for.uni <- make.y.for.uni(x1,x2,n)
my.summary(sqrt(n)*(0.5-make.par.for.uni(x1,x2,n)[,1]))
my.summary(sqrt(n)*(0.75-make.par.for.uni(x1,x2,n)[,2]))
n*solve(t(cbind(x1,x2))%*%cbind(x1,x2))

my.summary(make.par.for.uni(x1,x2,n)[,1])

t.test(sqrt(n)*(0.5-make.par.for.uni(x1,x2,n)[,1]),mu=0)

head(x1)
plot(sqrt(n)*(0.5-make.par.for.uni(x1,x2,n)[,1]))
hist(sqrt(n)*(0.5-make.par.for.uni(x1,x2,n)[,1]))
qqnorm(sqrt(n)*(0.5-make.par.for.uni(x1,x2,n)[,1]))
plot(density(sqrt(n)*(0.5-make.par.for.uni(x1,x2,n)[,1])))

t.test(c(10,10,10,10,10,10,10.001,10.000001),mu=10)

var(0.5-make.par.for.uni(x1,x2,n)[,1])*2000
var(sqrt(n)*(0.5-make.par.for.uni(x1,x2,n)[,1]))
sqrt(2000)
n
result.for.uni <- lm(y.for.uni~-1+x1+x2)
plot(predict(result.for.uni),result.for.uni$residuals)

1/((1.16)*0.25)

(1-0.36)/0.25

make.y.for.rand <- function(x1,x2,n){
  mu <- c()
  mu[1] <- rnorm(1)
  for(i in 1:(n-1)){
    mu[i+1] <- mu[i]+rnorm(1)
  }
  y <- 0.5*x1+0.75*x2+mu
  return(y)
}

make.par.for.rand <- function(x1,x2,n){
  mat <- matrix(0,100,2,byrow=T)
  for(i in 1:100){
    y <- make.y.for.rand(x1,x2,n)
    mat[i,] <- lm(y~-1+x1+x2)$coef
  }
  return(mat)
}  

mat
make.density(mat)

my.summary(mat[,1])
y <- make.y.for.rand(x1,x2,n)
plot(y)
#分散がばかでかい。
qqline(sqrt(n)*(0.5-mat[,1]))

n <- 200
x1 <- make.x1(n)
x2 <- make.x2(n)
mat <- make.par.for.rand(x1,x2,n)
my.summary(sqrt(n)*(0.5-mat[,1]))
my.summary(sqrt(n)*(0.5-mat[,2]))

curve(dcauchy,-100,100000)

rcauchy(1000)

make.y.for.cauchy <- function(x1,x2,n){
  mu <- rcauchy(n)
  y <- 0.5*x1+0.75*x2+mu
  return(y)
}

make.par.for.cauchy <- function(x1,x2,n){
  mat <- matrix(0,100,2,byrow=T)
  for(i in 1:100){
    y <- make.y.for.cauchy(x1,x2,n)
    mat[i,] <- lm(y~-1+x1+x2)$coef
  }
  return(mat)
}  

mat <- make.par.for.cauchy(x1,x2,n)
make.density(mat)
my.summary(mat[,1])
my.summary(mat[,2])

getwd()

setwd("/home/yasuhisa/Desktop/work/ts/img")
png("cauchy.density.png")
make.density(mat)
dev.off()