前回のところではガンベル分布からの乱数が生成できないとして、独立連鎖において正規分布を使って乱数生成をやった。しかし、上の記事の通り、全区間に渡って0以上となるような分布ならとりあえずできるらしいということが分かった。なので今回は独立連鎖の提案分布にt分布を使って、ガンベル分布からのサンプリングを行なってみようと思う。
というわけで早速コード。というか前回とあんまり変わっていない。
independent.chain <- function(c,N){ init <- 0 xt <- rep(NA,(N+1)) xt[1] <- init x <- rt(N,c) u <- runif(N) accept <- 0 for (i in 1:N){ a <- min(1, (exp(-abs(x[i])/3) * dt(xt[i],c)) / (exp(-abs(xt[i])/3) * dt(x[i],c)) ) if(u[i] < a){ xt[i+1] <- x[i] accept <- accept+1 }else{ xt[i+1] <- xt[i] } } return(list(accept=accept/N, xt=xt[((N/10)+1):(N+1)])) } plot.metropolis.hastings <- function(data,title){ accept <- data$accept xt <- data$xt par(oma=c(0,0,2,0)) par(mfrow=c(1,2)) title(main=title) plot(density(xt), main=paste("密度推定\n", "mean=",round(mean(xt),digits=2), ",var=",round(var(xt),digits=2) ) ) plot(xt,type="l") title("Iteration") mtext(side=3,line=-0.75,outer=T,text=paste(title,"\t(採択率:",round(accept*100),"%)",sep=""),cex=2) } plot.new() r <- independent.chain(1,10000) plot.metropolis.hastings(r,"独立連鎖") r <- independent.chain(3,10000) plot.metropolis.hastings(r,"独立連鎖") r <- independent.chain(5,10000) plot.metropolis.hastings(r,"独立連鎖") r <- independent.chain(10,10000) plot.metropolis.hastings(r,"独立連鎖")
前回は正規分布の分散がturning parameterでしたが、t分布の場合は自由度がturning parameterとなります。というわけで自由度1の場合こんな感じに。うまくサンプリングできていることが分かります。
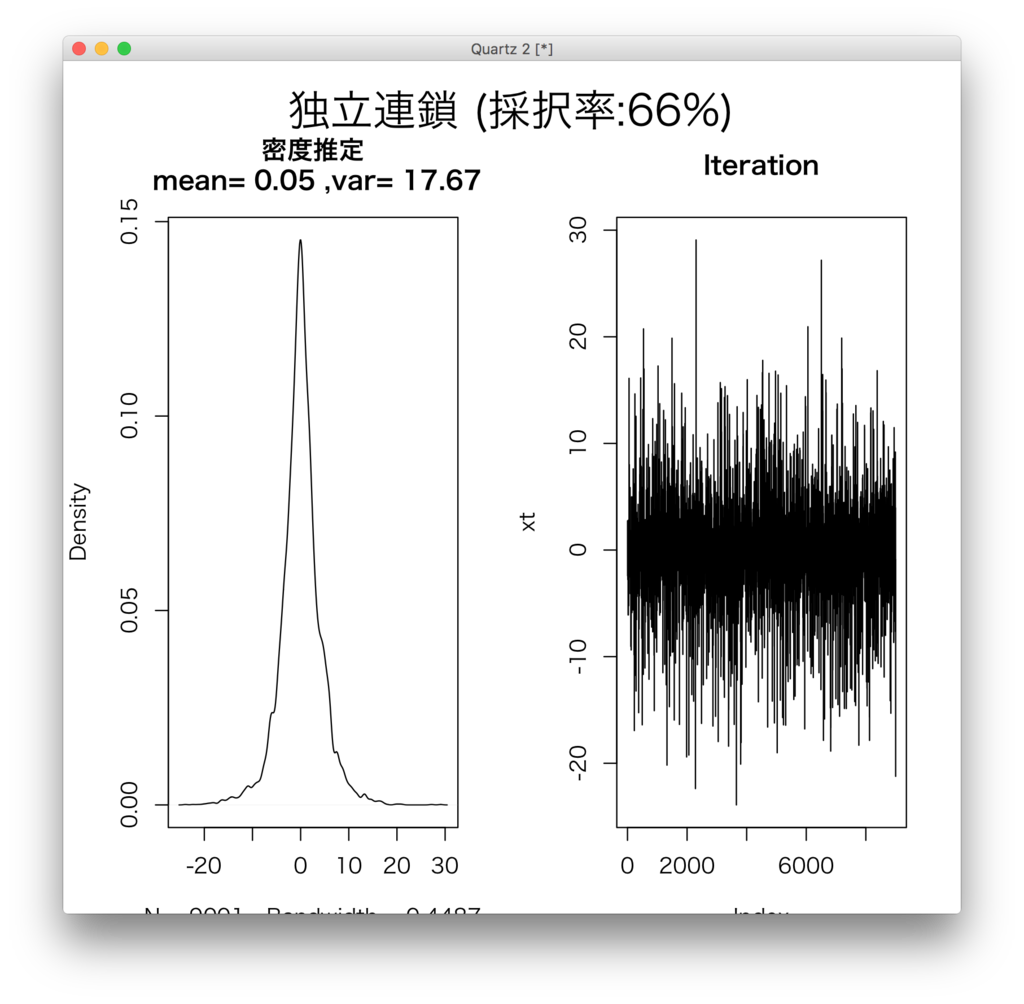
自由度20とかにするとこんな感じ。分散が全然ずれているし、iterationも途中で変な動きをしていることが分かりますね。
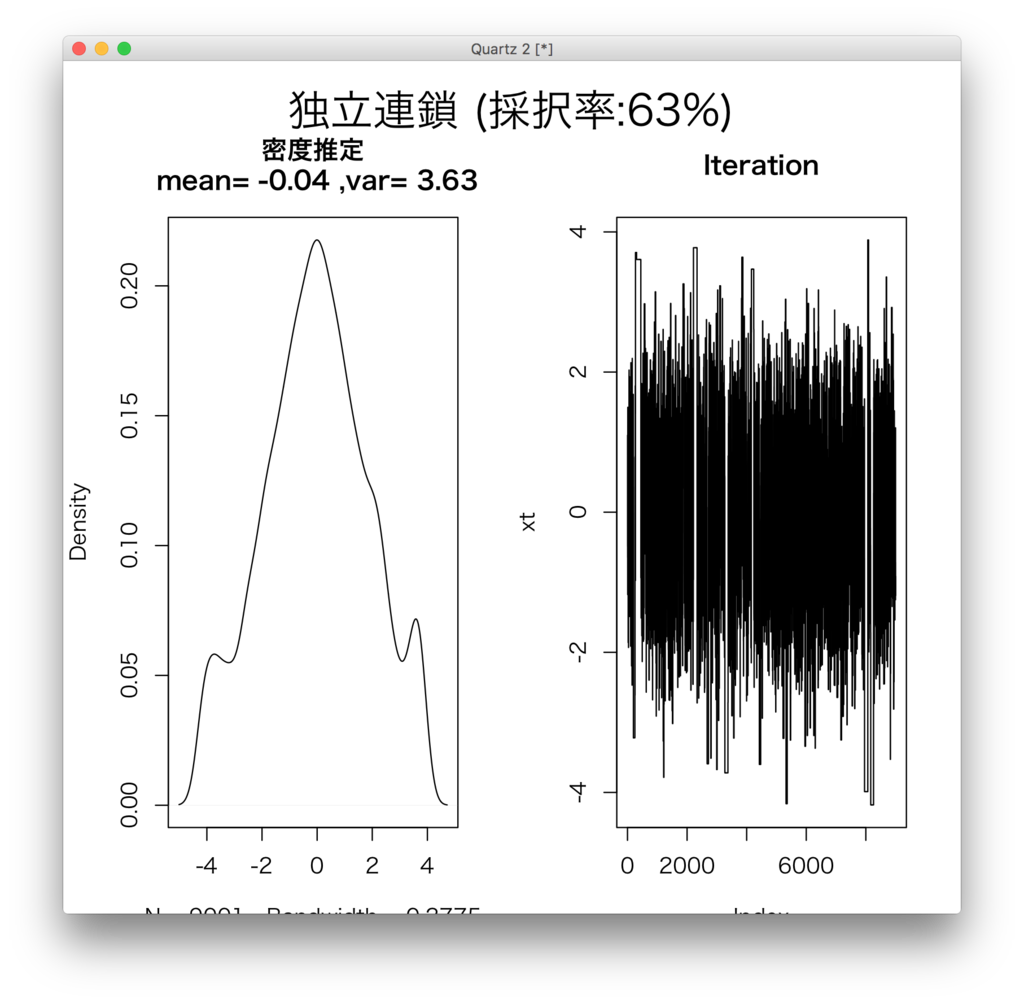
というわけで、全区間において0より大きいようなものからサンプリングしてくればMetropolis Hastings Algorithmの提案分布に使えそうだなあという感覚が持ててきました。まあ、turning parameterの問題とか、対象とする分布に提案分布がどれだけ近いかなどの問題はありますが。最初のステップは突破したかなという感じです。
自由度を変更すると?
一応載っけておこう。分散がやたら暴れるなあ。採択率はそれほど変わらないようだ。| c(自由度) | 平均 | 分散 | 採択率 |
|---|---|---|---|
| 1 | 0.004 | 17.67 | 67% |
| 3 | -0.22 | 15.38 | 55% |
| 5 | -0.05 | 12.7 | 49% |
| 10 | 0.43 | 9.83 | 47% |
| 20 | -0.2 | 4.52 | 55% |
初期値とBurn-inの関係
independent.chain関数の初期値を10とかにしていじめてみます。そうするとこんな感じになります。![Quartz 2 [*]](http://img.skitch.com/20090109-kd3ikra9qnd5b6nmhjxatbnf2q.jpg)
iterationのところを見ると初期値に長い強く期間影響を受けていることが分かります。そういうわけで最初のいくつかを取り除くというのが重要なんだなあということが分かります。