Example of Rejection Sampling

をやってみるてすと。PRMLの第11章サンプリング法のところのP242とかです。

Suppose we can not make the random samples which come from gamma distribution. Let us consider making them from the cauchy distribution. So proposal distribution is the cauchy distribution. The plot these distribution is as follows.

k <- 2.3
plot(function(x){dgamma(x,shape=10)},0,30,
     ylab="",col="red",lwd=3)
plot(function(x){k*dcauchy(x,scale=5,location=10)},0,30,add=TRUE,col="blue",lwd=3)
title(main="棄却サンプリング")
legend(15,0.12,c("ガンマ関数","一般化されたコーシー分布"),lwd=3,col=c("red","blue"))

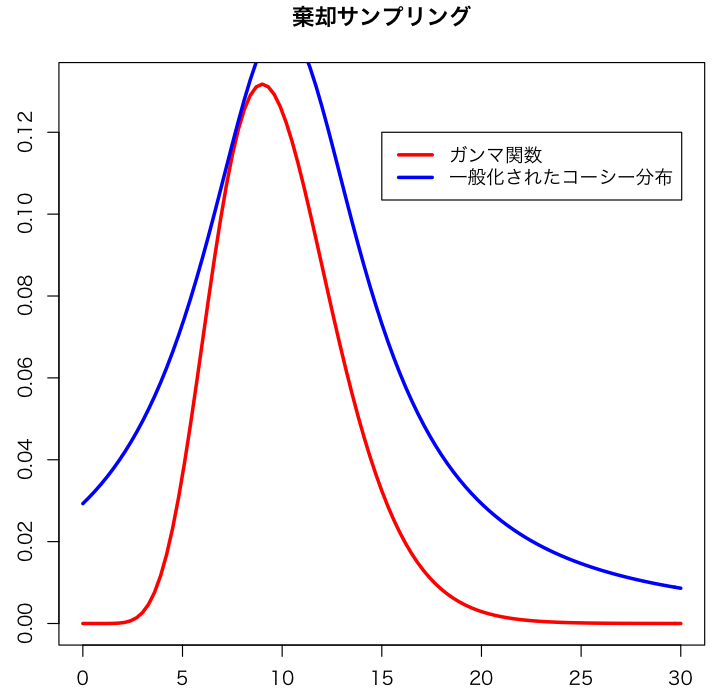
In the above case, the constant value $k$ is 2.3. For all x in the domain, the generalized cauchy distribution is greater than gamma distribution.

According to the マルコフ連鎖モンテカルロ法 (統計ライブラリー) in page 7-8, rejection sampling is written as,

Even if it is difficult to sample from the target distribution directly, we may get the random numbers from the target distribution indirectly using the distribution which we can sample easily. Such a method is called rejection sampling or accept-rejection sampling. Let $f(x)=Cp(x)$ . $p(x)$ represents the probability density function and C is the normalizing constant term which makes sum of $p(x)$ be equal to 1. When it is difficult to sample from $f(x)$ , suppose that there is the distribution function $g(x)$ which can easily generate the random numbers, and $g(x)$ has the constant value $M$ which satisfies $Mg(x) \geq f(x)$ . Under such assumptions, we can generate the random numbers from $f(x)$ indirectly as follows.

generate random number $x$ from $g(\cdot)$ .

calculate ratio $\alpha=f(x)/Mg(x)$ .

generate the uniform random number $\mu$ from interval $[0,1]$ .

adopt $x$ if $\mu < \alpha$ , otherwise return to 1.

And I implemented above algorithm with R. The program is as follows.

myrand <- function(){
  x <- rcauchy(1,scale=5,location=10)
  alpha <- dgamma(x,shape=10) / (k * dcauchy(x,scale=5,location=10))
  u <- runif(1)
  if(u < alpha){
    return(x)
  }else{
    print("false")
    myrand()
  }
}

n <- 1000
qqplot(rgamma(n,shape=10),sapply(1:n,function(x){myrand()}),xlab="random numbers from gamma distribution",ylab="random numbers from myrand")