Rを使った統計勉強法【中心極限定理編】

Rを使った統計の勉強法
中心極限定理とはなんぞや
- 要するに
正規分布
一様乱数で確認
正規分布に従っているか確かめよう
まとめ

Rを使った統計の勉強法

統計学の理論を、Rを使って本当に成立するか実験してみる
「なんで成立するのか」は置いといて、「どういうことを言っているのか」を体感する
- 「どういうことを言っているのか」を理解できれば、証明が何を言っているのかの理解しやすいかも

中心極限定理とはなんぞや

平均値 $\mu^{*}$ 、分散 $\sigma^{2*}$ を持つ、任意の分布に従う乱数列 $x_1,\cdots,x_n$ があるとき、その平均値 $\bar{x_n}=\frac{\sum_{k=1}^{n}x_k}{n}$ の確率分布は $n$ が大きくなる時、平均値 $\mu^{*}$ 、分散 $\sigma^{2*}/n$ である正規分布に収束する。

すなわち $\frac{\bar{x_n}-\mu^{*}}{\sigma^{*}/\sqrt{n}}$ は、nが大きい時、標準正規分布に従うとみなしてよい。

中心極限定理

要するに

何かしらの乱数があって
それをたくさん持ってくる
で、平均を取ると
正規分布っぽくなるよ

正規分布

次の式で表わされる確率密度関数のこと
$f(x)=\frac{1}{\sqrt{2\pi}\sigma}\exp(-\frac{(x-\mu)^2}{2\sigma^2})$

特徴

左右対称
つりがね状の曲線

plot(function(x,mu=0,sigma=1){1/(sqrt(2*pi)*sigma)*exp(-(x-mu)^2/2*sigma^2)},-3,3,ylab="確率密度",main="正規分布の確率密度関数")

plot(関数,範囲)のような形で関数をplotできます

muはmodeを変化させるパラメータ

norm <- function(x,mu=0,sigma=1){1/(sqrt(2*pi)*sigma)*exp(-(x-mu)^2/(2*sigma^2))}
par(mfrow=c(3,1))
plot(function(x){norm(x,mu=0,sigma=1)},-10,10,ylab="確率密度",main="正規分布の確率密度関数")
plot(function(x){norm(x,mu=3,sigma=1)},-10,10,ylab="確率密度",main="正規分布の確率密度関数")
plot(function(x){norm(x,mu=5,sigma=1)},-10,10,ylab="確率密度",main="正規分布の確率密度関数")

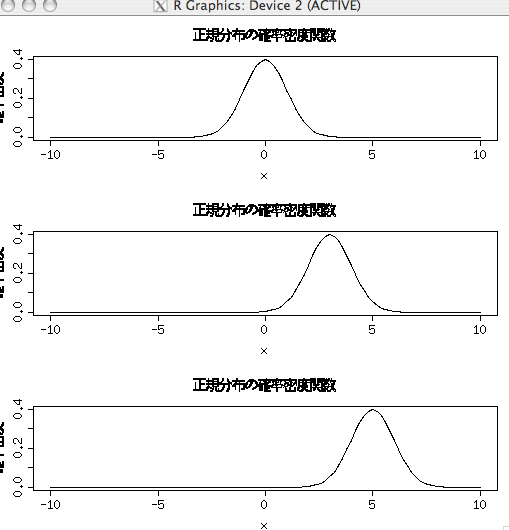
sigmaは分布のすそのを決めるパラメータ

par(mfrow=c(3,1))
plot(function(x){norm(x,mu=0,sigma=1)},-10,10,ylab="確率密度",main="正規分布の確率密度関数")
plot(function(x){norm(x,mu=0,sigma=2)},-10,10,ylab="確率密度",main="正規分布の確率密度関数")
plot(function(x){norm(x,mu=0,sigma=3)},-10,10,ylab="確率密度",main="正規分布の確率密度関数")

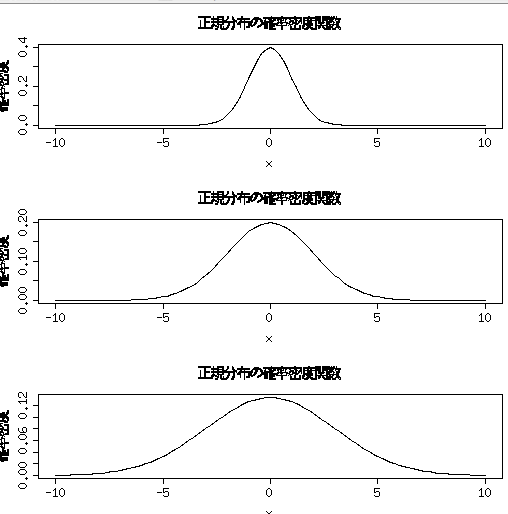
確認

何かしらの乱数があって
それをたくさん持ってくる
で、平均を取ると
正規分布っぽくなるよ

一様乱数で確認

一様分布はこんなの
- 離散だと、さいころとか

plot(dunif,-1,2,ylab="確率密度",main="一様の確率密度関数")

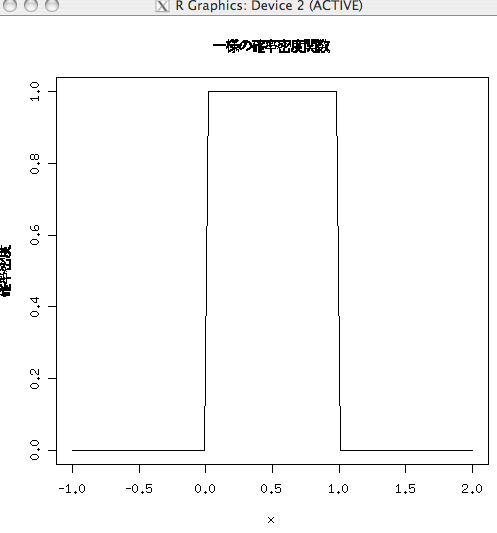
Rで一様乱数

runif(100)

par(mfrow=c(3,1))
hist(runif(10))
hist(runif(100))
hist(runif(1000))

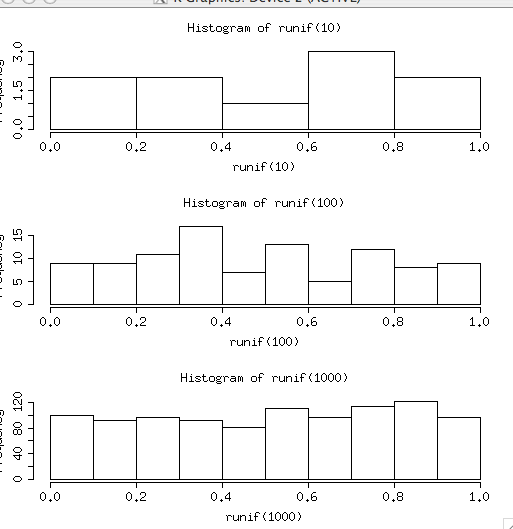
乱数の平均をいっぱい作る

100個の一様乱数の平均を100個作る

m <- c()
m
for(i in 1:100){
  m[i] <- mean(runif(1000))
}
m

めんどくさい人はこんなのどうぞ
- applyファミリーの使い方はあとで

sapply(seq(100),function(x){mean(runif(100))})

確認

何かしらの乱数があって
それをたくさん持ってくる
で、平均を取ると
正規分布っぽくなるよ

一様乱数の平均をたくさん取るところまではきた
あとは、このたくさんある平均が正規分布に従っているかを確認すればok

ヒストグラムで確認しよう

par(mfrow=c(2,2))
hist(sapply(seq(100),function(x){mean(runif(3))}),xlim=c(0,1))
hist(sapply(seq(100),function(x){mean(runif(5))}),xlim=c(0,1))
hist(sapply(seq(100),function(x){mean(runif(10))}),xlim=c(0,1))
hist(sapply(seq(100),function(x){mean(runif(100))}),xlim=c(0,1))

段々平均に寄ってくる

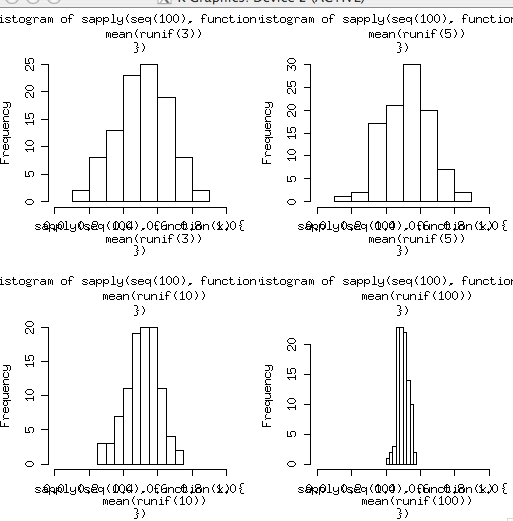
分かること
- nを増やしても平均は変わってない
  - まあ、当たり前か
- nを増やすと分散が小さくなっていく

戻ってみよう

お、なんか分かる気がする?

後半に行ってみよう

すなわち $\frac{\bar{x_n}-\mu^{*}}{\sigma^{*}/\sqrt{n}}$ は、nが大きい時、標準正規分布に従うとみなしてよい。

mu <- 1/2
sigma <- 1/12
n <- 100
(sapply(seq(1000),function(x){mean(runif(n))}) -mu) / (sigma/sqrt(n))
hist((sapply(seq(1000),function(x){mean(runif(n))}) -mu) / (sigma/sqrt(n)))

f:id:syou6162:20161128132406p:plain

正規分布っぽいね!

疑り深い人がいるかもしれない
「左右対象で、つりがね型っぽいけど本当に正規分布なのかよ?」
「コーシ分布とかかもしれねーじゃん」
- コーシー分布というのは、平均値を持たない恐ろしい(?)分布
- 期待値が発散してしまう→裾野が長い

コーシー分布

正規分布に従っているか確かめよう

正規分位点分位点プロット
qqplotとも呼ばれる

「分位点プロット」とはどういうものか

仕組みは簡単
2つの標本があって、その分布が同じものかどうか
「ある標本を小さい順に並び変えたもの」、「もう一つの標本の小さい順に並び変えたもの」を用意する
小さい順にそれぞれ取っていって、散布図を描いたもの
直線になれば、二つの分布は同じである、と見なす

正規分位点分位点プロット

「もう一つの標本」のほうに正規乱数を持ってきたもの

(sapply(seq(1000),function(x){mean(runif(n))}) -mu) / (sigma/sqrt(n))
rnorm(1000)

sort((sapply(seq(1000),function(x){mean(runif(n))}) -mu) / (sigma/sqrt(n)))
sort(rnorm(1000))

plot(sort((sapply(seq(1000),function(x){mean(runif(n))}) -mu) / (sigma/sqrt(n))),sort(rnorm(1000)))

f:id:syou6162:20161128132451p:plain

qqplot

qqplot((sapply(seq(1000),function(x){mean(runif(n))}) -mu) / (sigma/sqrt(n)),rnorm(1000))

「二つの分布を比較」ではなく、「ある分布が正規分布をしているか」を調べたい

qqnorm

qqnorm((sapply(seq(1000),function(x){mean(runif(n))}) -mu) / (sigma/sqrt(n)))
qqline((sapply(seq(1000),function(x){mean(runif(n))}) -mu) / (sigma/sqrt(n)))