プラグイン法による密度推定

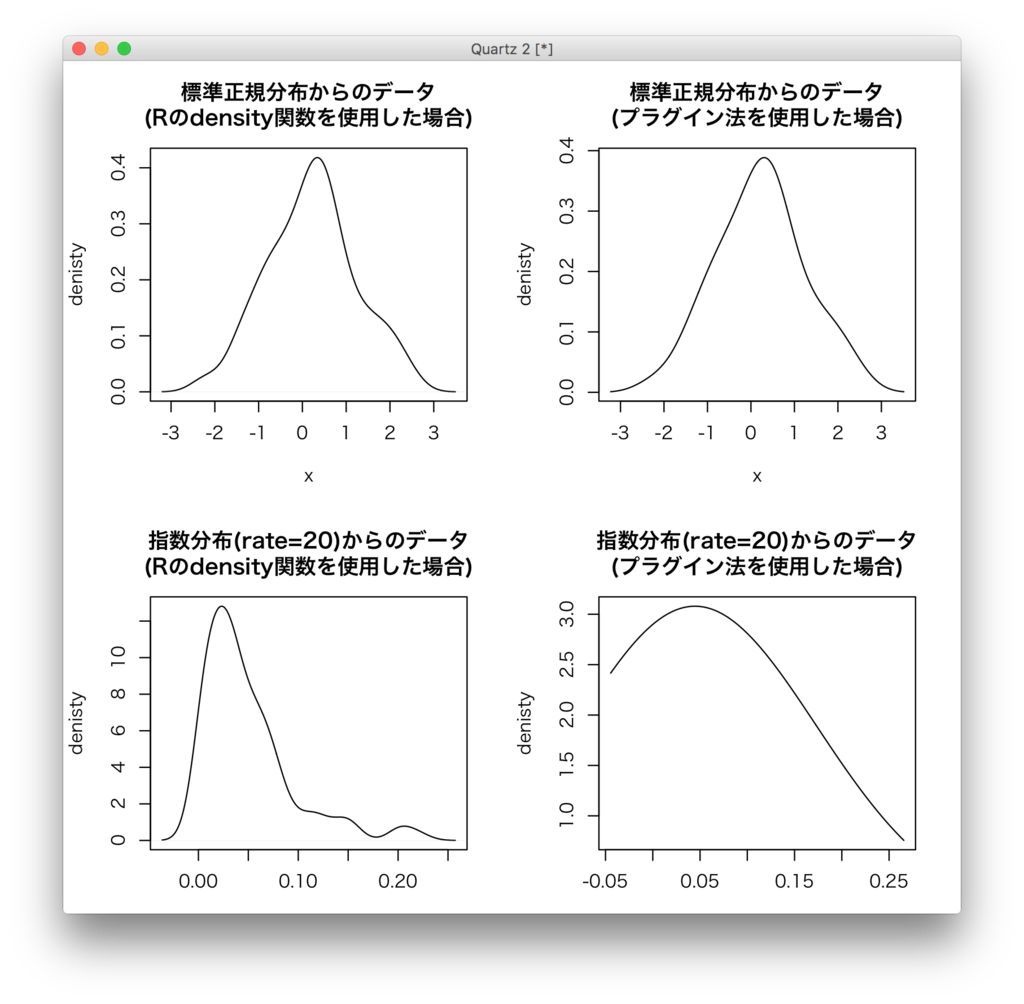
MSEを積分したMISEを最小にするhを使うとうまく密度推定できるよね!!という話があるんだけど、そのhには真の分布の二階微分が含まれており、だめじゃん＞＜という流れがある。仕方ないからノンパラなのに分布を仮定するプラグイン法というのがある。まあ、ノンパラだからそんなのだめじゃんっていう話があるんだけど、どうだめなのかを示すためのplot。真の分布を正規分布と勝手に仮定した上で最適にするhを決定する関数を適当に決めておいて、正規分布からのデータではある程度うまくいって、指数分布からのデータだとうまくいかなね＞＜ということを示している。

gauusian <- function(X,h){
  return(function(x){1/(length(X)*h) * 1/sqrt(2 * pi) * exp(-1/2 * ((x - X)/h)^2)})
}

optimal.h <- function(x){
  ((4*var(x)) / (3*length(x)))^(1/5)
}

par(mfrow=c(2,2))
#正規分布からのデータによる比較
x <- rnorm(100,0,1)
s <- seq(min(x)-sd(x),max(x)+sd(x),length.out=1000)
plot(density(x),
     xlab="x",ylab="denisty",
     main="標準正規分布からのデータ\n(Rのdensity関数を使用した場合)"
     )
plot(s,apply(sapply(s,gauusian(x,optimal.h(x))),2,sum)
     ,type="l",xlab="x",ylab="denisty",
     main="標準正規分布からのデータ\n(プラグイン法を使用した場合)"
     )

#指数分布からのデータによる比較
x <- rexp(100,rate=20)
s <- seq(min(x)-sd(x),max(x)+sd(x),length.out=1000)
plot(density(x),xlab="x",ylab="denisty",
     main="指数分布(rate=20)からのデータ\n(Rのdensity関数を使用した場合)"
     )
plot(s,apply(sapply(s,gauusian(x,optimal.h(x))),2,sum),
     type="l",xlab="x",ylab="denisty",
     main="指数分布(rate=20)からのデータ\n(プラグイン法を使用した場合)"
     )