多変数ナダラヤワトソン推定量を計算する関数を自前で実装した

先週は、1変数でのナダラヤワトソン推定量を計算していました。

今週は先生に「多変数でやってみな!!」と言われているので、こてしらべで2変数のをやってみました。

とりあえず回帰したい曲線があります。こんなの。muは正規分布に従う変数です。

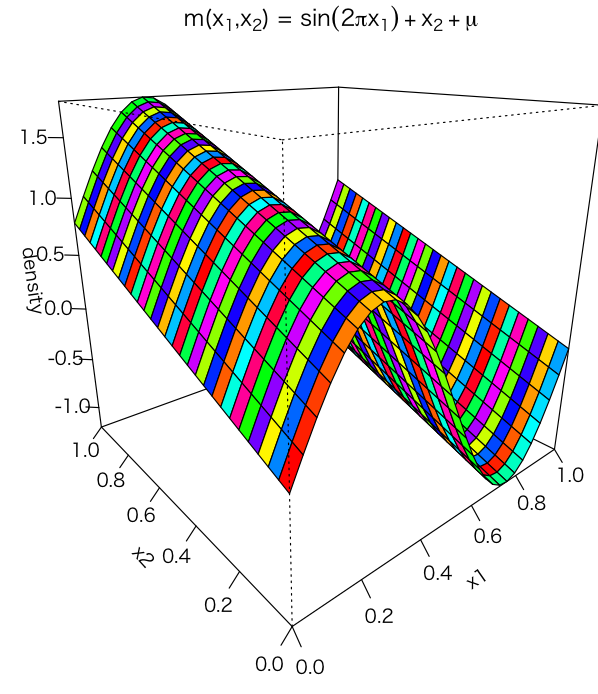
これをノンパラを使って、推定していきます。まだすごい制約をかけています。

幅に対する行列Hの非対角要素は0と仮定
乗法的カーネル関数を仮定
しかも、対角項のhはこちらで指定*1

とまあこんな制約の中でやっています。この制約のおかげで大分楽にできるようになります。カーネル関数はガウシアンを使っています。これさえ仮定しておけば、3変数以上もすぐにできそうです。p変数ある時にも
$\begin{eqnarray} \hat{m(X)} &=& \hat{E(Y|X=x)} \\ &=& \frac{\sum^n_{i=1} \frac{1}{|H|} K(H^{-1}(x-X_i))Y_i}{\sum^n_{i=1} \frac{1}{|H|} K(H^{-1}(x-X_i))} \\ &=& \frac{\sum^n_{i=1} \prod^p_{j=1}\exp(-\frac{1}{2} (x_j-X_{ji}))Y_i}{\sum^n_{i=1} \prod^p_{j=1}\exp(-\frac{1}{2} (x_j-X_{ji}))} \end{eqnarray}$
という式なので、まあどうにかできます。書きくだしてみれば、productのところが増えていくだけなので単純です。単純になるように、乗法的カーネル関数を仮定したわけですが。

で、推定してみた結果はこういう風になりました。

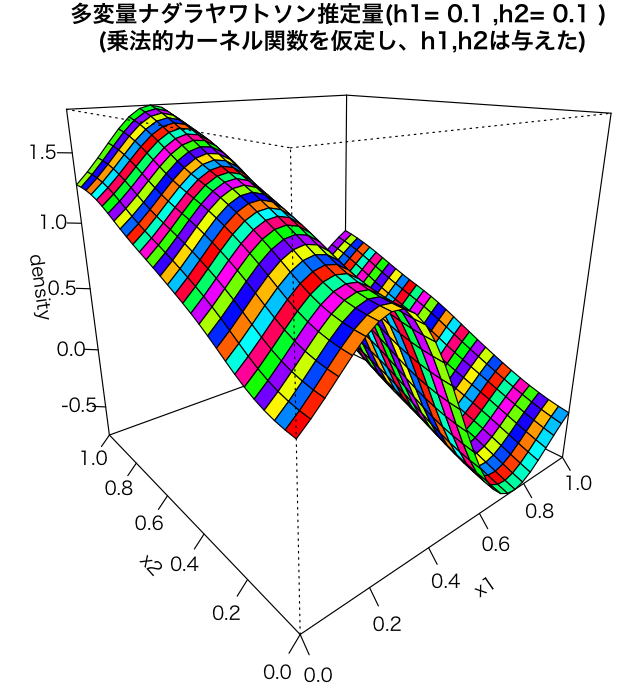
大体それっぽい感じですが、端点のところが結構ずれてますね。まあ、ナダラヤワトソンはそういうものだそうです。

#P133の曲線
mkr_with_noise<- function(x1,x2){
  return(sin(2*pi*x1)+x2+rnorm(1,0,1/4))
}

gauusian <- function(X1,X2,h1,h2){
  X1 <- X1
  X2 <- X2
  return(function(x1,x2){
    exp(-1/2 * ((x1 - X1)/h1)^2) * exp(-1/2 * ((x2 - X2)/h2)^2)
  })
}

y.exp <- function(X1,X2,Y,h1,h2){
  X1 <- X1
  X2 <- X2
  Y <- Y
  return(function(x1,x2){
    exp(-1/2 * ((x1 - X1)/h1)^2) * exp(-1/2 * ((x2 - X2)/h2)^2) * Y})
}

l <- 30
X1 <- seq(0,1,length=l)
X2 <- X1
Y <- outer(X1,X2,mkr_with_noise)

persp(X1,X2,Y,theta=320,phi=20,col=rainbow(50),
      main=expression(paste("m(",x[1],",",x[2],") = ",plain(sin) ( 2 * pi * x[1]) + x[2] + mu)),ticktype="detailed",
      xlab="x1",ylab="x2",zlab="density")



e <- expand.grid(X1,X2)
Y <- apply(e,1,function(x){
  x1 <- x[1]
  x2 <- x[2]
  mkr_with_noise(x1,x2)
})
X1 <- e[,1]
X2 <- e[,2]

h <- 0.1
h1 <- h
h2 <- h

s1 <- seq(0,1,length=l)
s2 <- seq(0,1,length=l)

persp(s1,s2,
      Reduce("+",Map(function(f){outer(s1,s2,f)},mapply(function(X1,X2,Y){y.exp(X1,X2,Y,h1,h2)},X1,X2,Y))) /
      Reduce("+",Map(function(f){outer(s1,s2,f)},mapply(function(X1,X2){gauusian(X1,X2,h1,h2)},X1,X2))),
      main=paste("多変量ナダラヤワトソン推定量(h1=",h1,",h2=",h2,")\n",
        "(乗法的カーネル関数を仮定し、h1,h2は与えた)"),
      theta=320,phi=20,col=rainbow(50),ticktype="detailed",
      xlab="x1",ylab="x2",zlab="density")

*1:最適なやつはまだ出すことができない