2変数でのカーネル密度推定の練習

2変数というとで先週書いた密度トレイスを参考にしました。が、微妙に間違いも発見しました。

• カーネル関数を使って密度トレイスを書いてみた→最後のほうに微妙に間違いがあるので注意!! - yasuhisa's blog

gauusian関数の仲の1/hにかかる括弧が抜けていた。一次元だとplotしたときにそんなに影響がなかったので、気がつかなかったが、次元増やしたら全然違うことになっていたので、先週の間違いに気がついた。

gauusian <- function(r,h){
  gauusian.intern <- function(r,h){
    return(paste("1/sqrt(2 * pi) * exp(-1/2 * ((x - ",r,")/h)^2)",sep=""))
  }
  eval(parse(text=paste("function(x){1/h * (",
               paste(sapply(r,function(s){gauusian.intern(s,h)}),collapse="+")
               ,")}")))
}

この辺を修正しつつ、2変数でのカーネル密度推定を実装してみました。

#自前で2変数でのカーネル密度推定を実装
gauusian <- function(X1,X2,h1,h2){
  gauusian.intern <- function(X1,X2,h1,h2){
    #カーネル関数の積
    return(paste("1/sqrt(2 * pi) * exp(-1/2 * ((x1 - ",X1,")/h1)^2)",
                 "*",
                 "1/sqrt(2 * pi) * exp(-1/2 * ((x2 - ",X2,")/h2)^2)",
                 sep=""))
  }
  eval(parse(text=paste("function(x1,x2){1/h1 * 1/h2 * (",
               #for suming up
               paste(mapply(function(X1,X2){gauusian.intern(X1,X2,h1,h2)},
                            X1,X2),collapse="+"),")}")))
}

n <- 1000
x <- rnorm(n)
y <- rnorm(n)
s1 <- seq(min(x),max(x),length.out=100)
s2 <- seq(min(y),max(y),length.out=100)
z <- outer(s1,s2,gauusian(x,y,0.1,0.1))

persp(s1,s2,z,theta=30,phi=30,col=rainbow(50),
      xlab="x1",ylab="x2",zlab="density",
      main=paste("2変数でのカーネル密度推定\n","h1=",h1,"\t","h2=",h2))

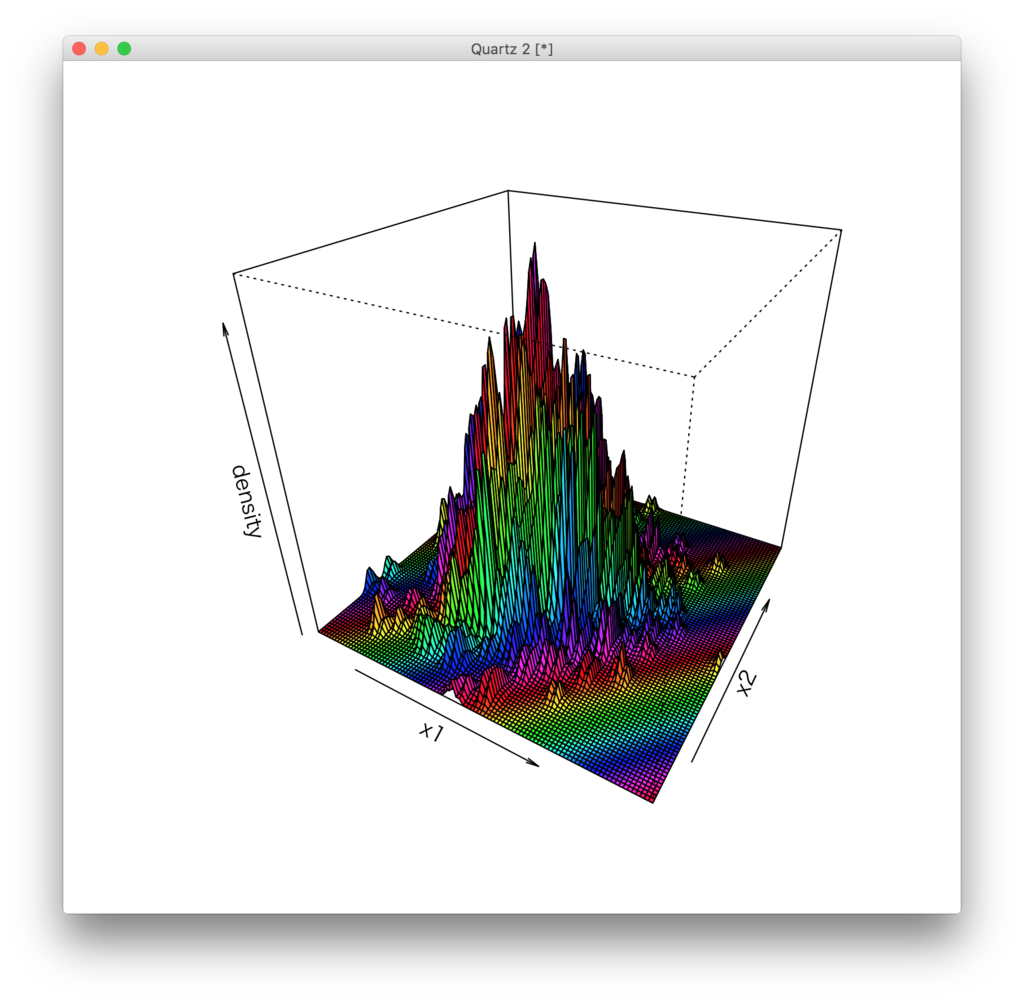
MASSパッケージのkde2d関数を使うとこんな感じでした。

persp(kde2d(x,y),col=rainbow(50),theta=30,phi=30,
      main=paste("2変数でのカーネル密度推定\n","h1=",h1,"\t","h2=",h2))

そんなに違わないかなー?密度トレイスより視覚化しての比較は難しくなってしまう。

遊ぶ

とりあえずお約束的にhを変えて遊んでみよう。はりせんぼんみたいなのが面白い。

h1 <- 1
h2 <- 1
z <- outer(s1,s2,gauusian(x,y,h1,h2))
persp(s1,s2,z,theta=30,phi=30,col=rainbow(50),
      xlab="x1",ylab="x2",zlab="density",
      main=paste("2変数でのカーネル密度推定\n","h1=",h1,"\t","h2=",h2))

h1 <- 0.01
h2 <- 0.01
z <- outer(s1,s2,gauusian(x,y,h1,h2))
persp(s1,s2,z,theta=30,phi=30,col=rainbow(50),
      xlab="x1",ylab="x2",zlab="density",
      main=paste("2変数でのカーネル密度推定\n","h1=",h1,"\t","h2=",h2))

追記

文字列の結合で巨大な関数作り出すのは時間がかかるよね*1、っていうのをこの前の最後の付近に書いておいたにもかかわらず、またやっていた。というわけで別に間違っているわけじゃないんだけど、書きなおしておいた。計算時間的な意味で。

gauusian <- function(X1,X2,h1,h2){
  X1 <- X1
  X2 <- X2
  return(function(x1,x2){exp(-1/2 * ((x1 - X1)/h1)^2) * exp(-1/2 * ((x2 - X2)/h2)^2) })
}

n <- 1000
x1 <- rnorm(n)
x2 <- rnorm(n)
s1 <- seq(min(x1),max(x1),length.out=100)
s2 <- seq(min(x2),max(x2),length.out=100)

h1 <- 0.2
h2 <- 0.2

y <- Reduce("+",Map(function(f){outer(s1,s2,f)},mapply(function(X1,X2){gauusian(X1,X2,h1,h2)},x1,x2)))

persp(s1,s2,y,theta=320,phi=20,col=rainbow(50),
      xlab="x1",ylab="x2",zlab="density",
      main=paste("2変数でのカーネル密度推定\n","h1=",h1,"\t","h2=",h2))

*1:最急降下法とかで持っておかない場合を除く