最急降下法で最適なバンド幅を計算してみた

ナダラヤワトソン推定量は計算できたわけですが、これにはまだバンド幅hを決めるという問題が残っています。バンド幅を最適なものにする*1ための一つの尺度として、最小二乗クロスバリデーション評価関数を最小にするようにhを選択する、という方法があります。最小二乗クロスバリデーション評価関数というのは以下の式のことです。
$CV(h_x) = \sum^n_{i=1}(Y_i - (\frac{\sum^n_{j=1,j \neq i}K_X(\frac{X_i-X_j}{h_x})Y_j}{\sum^n_{j=1,j \neq i} K_X(\frac{X_i-X_j}{h_x})}))^2$
これを最適にするhは妥協しなかった時の(?)やつと比較して収束性とかその辺を考えるとわりとよいものらしいです(この辺よく分かってない)。まあ、性質は示されているので、僕の今の仕事は最小二乗クロスバリデーション評価関数を最小にするhをいかにして決めるかというもの。

僕が使える最適化の手法と言ったら最急降下法くらいなんですが(そういえば遺伝的アルゴリズムも使えることは使えるか)、この問題は $h \neq 0$ という以外には制約がなさそうなので、最急降下法がどうやら使えそうです。最急降下法を使うためには、最小二乗クロスバリデーション評価関数の微分が分からないといけないわけですが、これをまともに出そうとすると死ぬ。いや、できるけどそれを生成させるRのコードが死にます。でも、Rには数式微分が使えます。なのでデータX、Yが与えられたら最小二乗クロスバリデーション評価関数を生成する関数を作ればどうにかできるわけです。

そんなわけでごりごりと書きました。微分のことがあるので、使い勝手がよさそうなガウシアンカーネルを採用することにしました。cv関数とかをなにげなく走らせると、こんなことになるので注意が必要ですw。

gauusian <- function(X,h){
  return(function(x){1/(length(X)*h) * 1/sqrt(2 * pi) * exp(-1/2 * ((x - X)/h)^2)})
}

y.exp <- function(X,Y,h){
  return(function(x){1/(length(X)*h) * 1/sqrt(2 * pi) * exp(-1/2 * ((x - X)/h)^2) * Y})
}

y.exp.for.support <- function(Xj,Yj){
  y.exp.for.support.intern <- function(Xj,Yj){
    return(paste("exp(-1/2 * ((Xi - ",Xj,")/h)^2) * ",Yj,sep=""))
  }
  paste(paste(mapply(function(Xj,Yj){y.exp.for.support.intern(Xj,Yj)},Xj,Yj),collapse=" + ")," - Yi")
}

gauusian.for.support <- function(Xj){
  gauusian.for.support.intern <- function(Xj){
    return(paste("exp(-1/2 * ((Xi - ",Xj,")/h)^2)",sep=""))
  }
  paste(paste(sapply(Xj,function(Xj){gauusian.for.support.intern(Xj)}),collapse=" + "),"- 1")
}

cv <- function(Xi,Yi){
  x <- Xi
  y <- Yi
  cv.intern <- function(Xi,Yi){
    y <- gsub("Yi",as.character(Yi),gsub("Xi",as.character(Xi),y.exp.for.support(x,y)))
    g <- gsub("Xi",as.character(Xi),gauusian.for.support(x))
    return(paste(Yi," - ((",y,")/(",g,"))",sep=""))
  }
  paste("(",paste(mapply(function(Xi,Yi){cv.intern(Xi,Yi)},Xi,Yi),collapse=" + "),")^2")
}

decide.support <- function(x,y,h=0.1,epsilon=0.9,tau=0.9){
  #最急降下法
  f <- eval(parse(text=paste("expression(",cv(x,y),")")))
  D.sc <- eval(parse(text=paste("D(expression(",cv(x,y),"),\"h\")")))
  beta <- 1
  n <- 200
  for(i in seq(n)){
    nabla_f <- (function(h){eval(D.sc)})(h)
    while((function(h){eval(f)})(h - beta * nabla_f) >
          (function(h){eval(f)})(h) - epsilon * beta * nabla_f^2){
      beta <- tau * beta
    }
    a <- beta
    h <- h - a * (function(h){eval(D.sc)})(h)
    cat(paste(h),fill=T)
  }
  #バンド幅はプラスマイナスのどっちでもいい。左右対称であるし、indicator functionの絶対値のところで影響が消えるから
  return(abs(h))
}

で、これがきちんと動いているかとかを確かめる。carsのデータでやってみました。最小二乗クロスバリデーション評価関数はまがまがしい形をしていますが、所詮hのだけの1変数関数です。だから、plotしてやれば大体の目安はつく。

x <- cars$speed
y <- cars$dist
plot((function(h){eval(eval(parse(text=paste("expression(",cv(x,y),")"))))}),0,4,xlab="h",ylab="評価関数の値")

f:id:syou6162:20161103172412p:plain
plotしてみるとなんだか行けそうな気がしてくるから不思議。2くらいと辺りを付けてやってみるか*2。1.9くらいから始めさせてみる。

h <- decide.support(x,y,h=1.9,epsilon=0.9,tau=0.9)

ちゃんとそれっぽいところにいっていることが分かる。途中から値が変化しなくなっているので収束していることが確認できます。

> h
[1] 2.000085

このhを使った上で平滑化曲線をplotしてみました。

plot(x,y,xlab="speed of cars",ylab="dist of cars")
title(main="Rの平滑化関数と自前の関数の比較\n(hは最小二乗クロスバリデーションで決定)",
      sub=paste("(h = ",h,")",sep=""))
lines(lowess(x,y),col="red")

s <- seq(min(x),max(x),length.out=1000)
g <- apply(sapply(s,gauusian(x,h)),2,sum)
y <- apply(sapply(s,y.exp(x,y,h)),2,sum)
lines(s,y/g,col="blue")
legend(4,110,c("Rのlowess","自前の平滑化曲線"),lwd=1,col=c("red","blue"))

f:id:syou6162:20161103172531p:plain
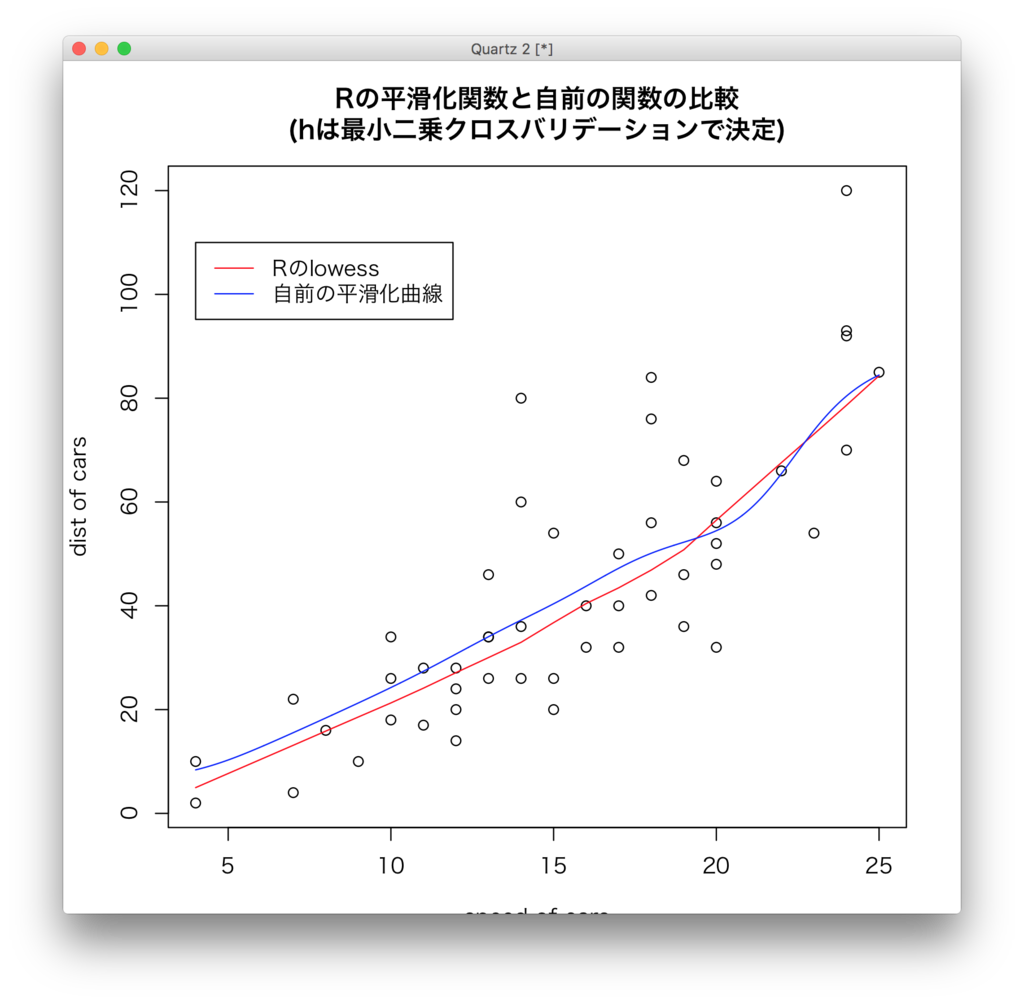
Rのlowessと同程度ってところかな。恣意的にhを与えるよりこっちのほうがよさそう。Rのlowessがどういう風にバンド幅を出しているかとかは先生に聞いてみるかー。というわけで、ノンパラでの単回帰は実装こんなところで終わりにしておこう。これが後でどれくらい生きてくるか。。。