Confidence interval for kernel density estimator

お、なんか大分間が空いた気がする。

修論スタート、ということでノンパラな推定量に関しての信頼区間の付近を準備しています。とりあえず今は一番簡単そうなカーネル密度推定の1変数のバージョンの信頼区間。週末とかに「分からねー」を連発しながらやってたんですが、やっとのことで

という定理の証明が追えたので、これを元に信頼区間をplotするスクリプトをこしらえてみました。

というわけでプログラム。

epanechnikov <- function(X1,h1){
  X1 <- X1
  h1 <- h1
  return(function(x1){
    u <- (x1 - X1)/h1
    if(1 > abs(u)){
      return(0.75 * (1-u^2))
    }else{
      return(0)
    }
  })
}

density.estimator <- function(X1,h,length.out=30){
  s <- seq(from=min(X1),to=max(X1),length.out=length.out)
  1 / (length(X1) * h) * apply(sapply(s,
               function(x){
                 mapply(
                        function(f){
                          f(x)
                        },mapply(
                                 function(X1){
                                   epanechnikov(X1,h)
                                 },X1)
                        )
               }
               ),2,sum)
}

confidence.interval <- function(X1,h,length.out=30){
  s <- seq(from=min(X1),to=max(X1),length.out=length.out)
  fhatx <- density.estimator(X1,h=h,length.out=length.out)
  upper <- fhatx + 1.96 * (length(X1)*h)^(-1/2) * (fhatx * 3/5)^(1/2)
  lower <- fhatx - 1.96 * (length(X1)*h)^(-1/2) * (fhatx * 3/5)^(1/2)
  return(list(fhatx=fhatx,upper=upper,lower=lower))
}

X1 <- cars$speed
n <- 30
s <- seq(from=min(X1),to=max(X1),length.out=n)

h <- 7
c <- confidence.interval(X1,h=h,length.out=n)
d <- c$fhatx
u <- c$upper
l <- c$lower
plot(s,d,ylim=c(min(d)-0.02,max(d)+0.02),type="l")
lines(s,u,col="red")
lines(s,l,col="red")

で、とりあえずこんな感じで信頼区間を求めるところまではできました。

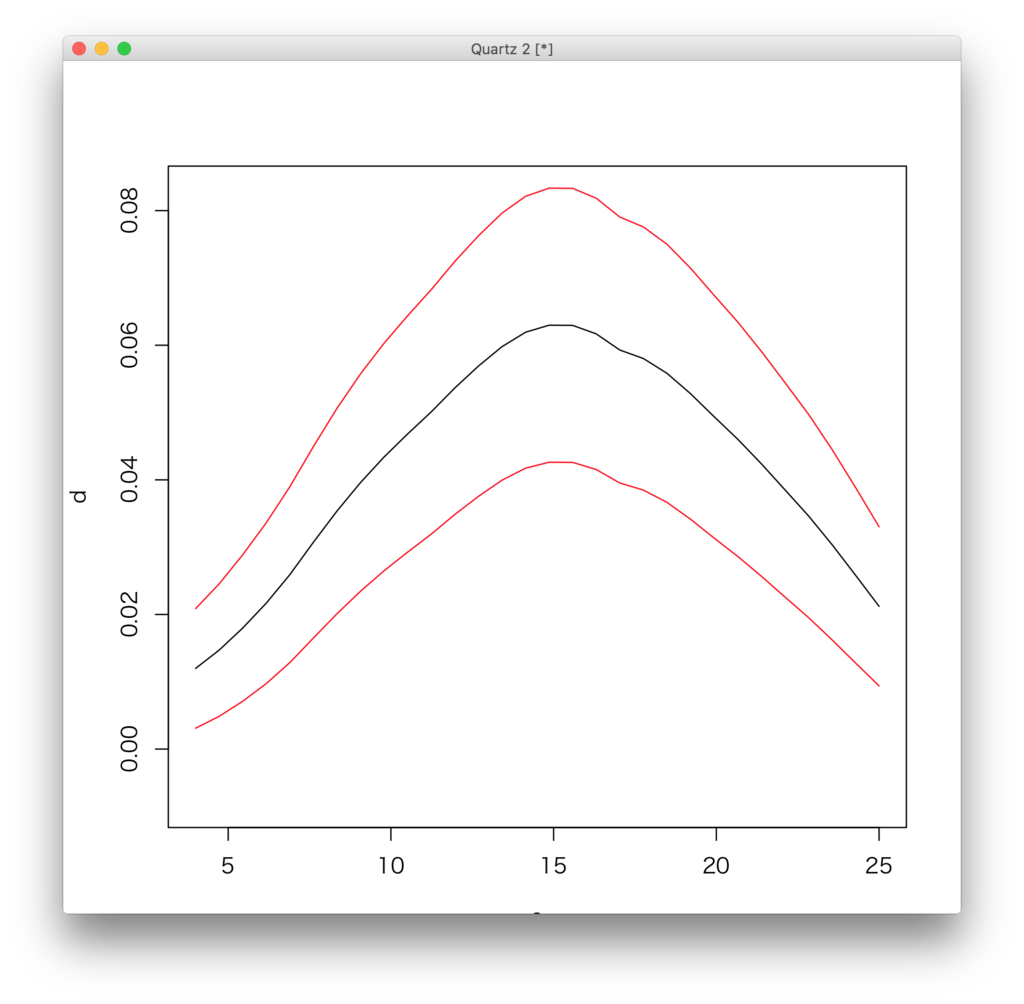
今のところは最適なバンド幅は求めないで適当に使っているんですが、その辺もやってみよう…と思ったんですが、よく考えたらクロスバリデーション最小化はナダラヤワトソンのやつしかやったことがないということを思い出した。密度推定のほうのクロスバリデーションは畳み込みが入ってくるため数値積分の関数をこしらえないといけないんだった。