正規分布の和の分布と、混合正規分布の違い

なんか中学生が分からない、とか言ってそうな内容ですが。大学4年で分かってないのでRでやってみた。

正規分布の和の分布

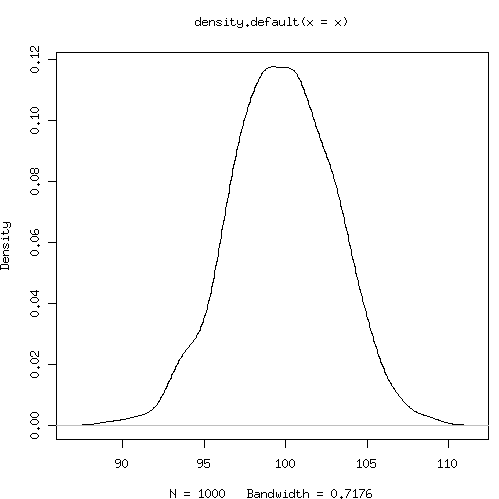
最初はこっちが出てくるのをなかなか理解できない(たぶん)っていう例のほう。二山になる、かと思うんだけど違うんだよね。平均と分散も理論値とほぼ一緒。いわゆる再生性というやつですね。

> x <- rnorm(m=0,sd=3,n=1000)+rnorm(m=100,sd=1,n=1000)
> (function(x){return(list(mean(x),var(x)))})(x)
[[1]]
[1] 100.0517

[[2]]
[1] 10.12451

> plot(density(x))

混合正規分布

http://www.okada.jp.org/RWiki/?R%A5%B3%A1%BC%A5%C9%A4%CE%BA%C7%C5%AC%B2%BD%CE%E3%A1%A7%BA%AE%B9%E7%C0%B5%B5%AC%CD%F0%BF%F4%A4%CE%C8%AF%C0%B8%A5%B3%A1%BC%A5%C9

この辺を参考にした。違いが分かりやすいようにパラメータをいじった。

> generator <- function(n) {
+    data1 <- rnorm(n)-1           # N(-1,1) に従う乱数
+    data2 <- rnorm(n)+20           # N(20, 1) に従う乱数
+    data3 <- (runif(n) <= 0.6)    # 確率 0.6 で 1 となる論理ベクトル
+    data1*data3 + data2*(1-data3) # 確率 0.6 で N(-1,1), 確率0.4で N(2,1) 乱数を採択
+ }
> 
> x <- generator(1000)
> (function(x){return(list(mean(x),var(x)))})(x)
[[1]]
[1] 7.705555

[[2]]
[1] 108.1045

> plot(density(x))

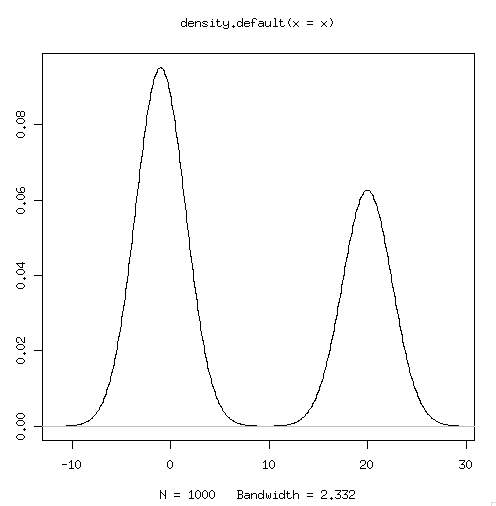
で、違いは?

最初、よく分からなかったんだけどコード見てたらなんか分かってきた。この部分。

> (runif(100)<=0.6)
  [1] FALSE  TRUE  TRUE  TRUE  TRUE  TRUE FALSE FALSE FALSE  TRUE  TRUE  TRUE
 [13] FALSE  TRUE FALSE  TRUE FALSE FALSE FALSE  TRUE  TRUE  TRUE  TRUE  TRUE
 [25]  TRUE  TRUE FALSE FALSE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE FALSE
 [37] FALSE FALSE  TRUE  TRUE  TRUE  TRUE FALSE  TRUE  TRUE  TRUE  TRUE  TRUE
 [49]  TRUE FALSE  TRUE FALSE  TRUE  TRUE FALSE  TRUE  TRUE FALSE  TRUE  TRUE
 [61]  TRUE  TRUE  TRUE  TRUE FALSE  TRUE FALSE  TRUE  TRUE  TRUE FALSE FALSE
 [73] FALSE FALSE  TRUE FALSE FALSE  TRUE  TRUE  TRUE FALSE  TRUE FALSE  TRUE
 [85] FALSE  TRUE  TRUE  TRUE FALSE FALSE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE
 [97]  TRUE  TRUE  TRUE  TRUE

もしや…と思って調べてみるとやっぱりそうだった。

> 1-(runif(100)<=0.6)
  [1] 1 0 1 1 0 0 0 1 0 0 1 1 0 0 1 1 1 0 1 0 1 0 0 0 0 0 0 0 1 0 0 0 1 0 0 0 0
 [38] 0 1 1 0 0 1 1 1 0 1 0 0 0 0 0 0 1 0 0 1 0 1 1 1 0 0 0 0 0 1 0 0 1 1 1 0 1
 [75] 1 1 0 0 0 0 0 1 0 0 0 1 0 0 0 1 0 0 0 1 0 0 0 1 0 0

こういう感じで解釈されてるってことね。

> as.numeric((runif(100)<=0.6))
  [1] 0 0 0 1 0 1 1 1 0 0 0 1 0 1 0 1 0 1 0 0 1 1 0 0 1 1 0 1 1 1 1 1 1 0 1 1 0
 [38] 0 0 0 1 0 1 1 0 1 1 1 1 0 1 0 0 1 1 0 0 0 1 1 0 0 1 0 1 0 0 0 1 0 0 1 1 1
 [75] 0 1 1 0 1 1 1 1 0 1 1 1 1 0 1 1 0 1 1 0 1 0 0 1 0 1

これから分かることは?

混合正規分布のほうでは、割合が取られているということだ。一方に0.4の重みを、もう一方に0.6の重みを付けている。それに従う乱数というのはその割り合いで取るか取らないか、ということが行われている。

「じゃあ、混合正規分布の割り合いを0.5と0.5にしたら同じなの?」という疑問が起こるが、これは違う。

> x <- 0.4*rnorm(m=0,sd=3,n=1000)+0.6*rnorm(m=100,sd=1,n=1000)
> (function(x){return(list(mean(x),var(x)))})(x)
[[1]]
[1] 59.88259

[[2]]
[1] 1.915873

> plot(density(x))