集合列の上極限と下極限

ボレル集合体とかをちょっと離れて、道具の準備をすることにする。集合列の上極限と下極限とかいうのがいみふすぐるので、どうにかする。

上極限集合と下極限集合の定義

集合列 $A_1,\cdots,A_n,\cdots$ が与えられた時
$\limsup_{n\to\infty}A_n=\cap^\infty_{n=1}\cup^\infty_{k=n}A_k$
$\liminf_{n\to\infty}A_n=\cup^\infty_{n=1}\cap^\infty_{k=n}A_k$
とおき、 $\limsup_{n\to\infty}A_n$ と上極限集合、 $\liminf_{n\to\infty}A_n$ を下極限集合という。

capとcupの順番とかそもそもどういうものなのかよく分からない。

ルベーグ積分30講 (数学30講シリーズ)のP81くらいに戻る。 $x \in \limsup_{n\to\infty}A_n$ というのは、どんなnを取っても常に
$x \in \cup^\infty_{k=n}A_k$ が成立するというとである、と書いてある。え、意味が分からない。。。

で、色々探したけど、ときわ台学/ルベーグ積分/上極限集合と下極限集合の例が分かりやすかった。例えば
$A_k = \{(x,y)|x^2 + y^2 \leq (1 - (-1)^k / k)^2 \}$
のような集合列を考える。これは増えたり、減ったりしながら収束していく。こんな感じ。

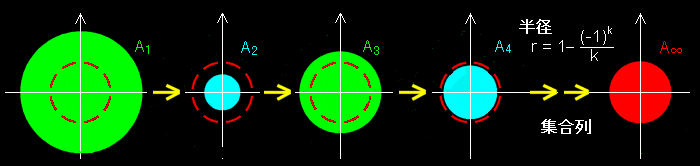
で、上極限というのはこういうもの。 $\cup^\infty_{k=1}A_k$ とかは和集合だから、外側のやつなんだけど、kを増やしていって、かつ、積集合を取っていくと赤の円のところに収束していく。上から抑えに行っていて、上極限の名前にあっているような感じ。

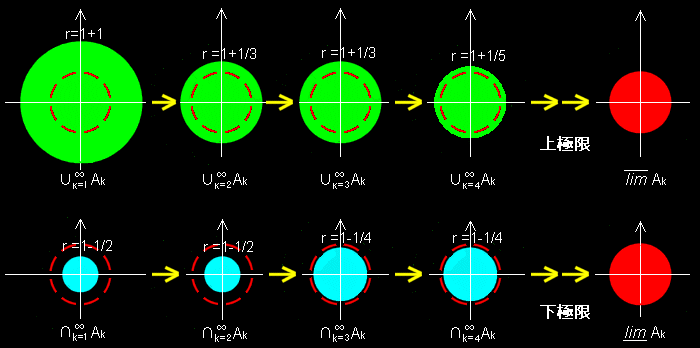
で、下極限のほうは $k \to \infty$ の時までの積集合を考えていて、最初は一番小さい。で、あとはkを増やしていって和集合を取っていく。ということで、どんどん大きくなるんだけど、赤のところまでしか行けなくって、そこに収束する下極限のイメージにあってるな。