まあ、一例を見たからと言って確かめたことにならないから証明するわけだが。一例をやってみて、理解を深めるというのはあるのでやってみるテスト。
『が平均
、分散
の正規分布に、
が平均
、分散
の正規分布に従い
、
が独立であるとすると、
という確率変数は平均
、分散
の正規分布に従う』という性質があり、これは正規分布の再生性と呼ばれる性質である*1。
RでこのZに当てはまるような適当な変数を作ってみる。
> rand<-rnorm(1000,mean=1,sd=3)*10+rnorm(1000,mean=9,sd=20)*3
理論値を計算してみると平均37、標準偏差67くらいなので、それをパラメータとして持つ正規分布と並べてみる。
> hist(rand,prob=TRUE) > curve(dnorm(x,mean=37,sd=67),add=TRUE)
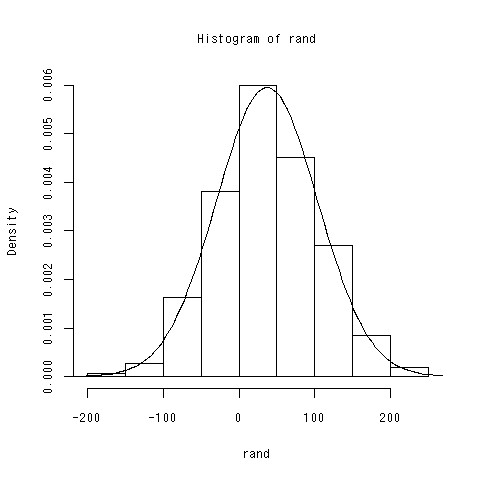
おお、何かそれっぽい感じになったなった。
ちなみにrandの平均と標準偏差は
> mean(rand) [1] 37.28064 > sd(rand) [1] 67.67154
ということでおkでしょう。なんかこういうの金融リスク管理論の課題とかに思いっきりあった気がするなぁ。Excelとかでやってた気が。。。
ええっと、だからどうなのかって言われると、R勉強会の準備のやつをちょっと出してみただけです。それだけ。練習問題とかでこれくらいやってもらおうかなぁ。みんな頭いいから楽勝っすよね。再生性の証明とかもやってもらうようにすれば、統計勉強会のネタにもなるぞw。
追記
自分に課題出しとこ。明日のR勉強会が終わったら解いてみる。
ポアソン分布が再生性を持つことを証明し、上の正規分布でやったように理論と一致するか確かめてみよ。
ヒントとしては2つのポアソン分布の積率母関数を出して、それらの積を取ったものが、またポアソン分布の積率母関数になっている、ということを示せればよいはず*2。Rの方はdpoisでパラメータlambdaと書いておけばこれで全て。誰か解いてくれといても全然構わない。
今見たら、ほぼ同じような問題が去年の応用確率論の中間レポートにあること発見。去年はいみふだったなー。