資料はここだよ!!
R勉強会第二回
- Presented by 吉田康久
前回は?
- Rの基本的なところ
- 基本統計量
- 分布の見方
- 簡単データ解析
- 関数
- 検定
- etc
今回は?
- Rのデータ型、データ構造、知ってると便利な関数とかを紹介
- 主にデータ構造の話
- どういうものなの
- どうやって作るの
- どうやって使うの
- 前回よりちょっとマニアックな話…かも
- でも、使いこなす上では避けては通れない道
- がんばりませう
データ型
- 実数
- 整数
- 複素数
- 文字列
- 論理型
データ型を調べる
- mode関数
- データ型を調べる
> a<-c(1,2,3,4) > mode(a) [1] "numeric"
データ構造
- ベクトル
- 行列
- 配列
- リスト
- データフレーム
- 順序なし因子
- 順序つき因子
たくさんある><
- ひとつひとつ見ていきます
ベクトル
- c関数とかでできるやつ
- Rにはスカラーはないよ
> mydata<-c(2.9,3.4,3.4,3.7,3.7,2.8,2.8,2.5,2.4,2.4)
いろんなベクトルの作り方
- 自分の手で打つのが面倒なやつとか
- 乱数をベクトルにするとか
規則的データの生成
- seq関数
- 第一引数から第二引数まで
- byの間隔で数列を作る
> seq(1,10,by=0.1) [1] 1.0 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.9 2.0 2.1 2.2 2.3 2.4 [16] 2.5 2.6 2.7 2.8 2.9 3.0 3.1 3.2 3.3 3.4 3.5 3.6 3.7 3.8 3.9 [31] 4.0 4.1 4.2 4.3 4.4 4.5 4.6 4.7 4.8 4.9 5.0 5.1 5.2 5.3 5.4 [46] 5.5 5.6 5.7 5.8 5.9 6.0 6.1 6.2 6.3 6.4 6.5 6.6 6.7 6.8 6.9 [61] 7.0 7.1 7.2 7.3 7.4 7.5 7.6 7.7 7.8 7.9 8.0 8.1 8.2 8.3 8.4 [76] 8.5 8.6 8.7 8.8 8.9 9.0 9.1 9.2 9.3 9.4 9.5 9.6 9.7 9.8 9.9 [91] 10.0
同じデータを繰り返す
- rep関数
- 第一引数のデータを
- times回繰り返す
> rep(c("a","b","c"),times=10) [1] "a" "b" "c" "a" "b" "c" "a" "b" "c" "a" "b" "c" "a" "b" "c" "a" "b" "c" "a" [20] "b" "c" "a" "b" "c" "a" "b" "c" "a" "b" "c"
ベクトルへのアクセスの方法
- []
- シーケンスを投げると、そこの部分をベクトルにして返してくれる
> mydata[5] [1] 3.7 > mydata[3:5] [1] 3.4 3.7 3.7
アクセス方法にもいろいろある
- 論理値でTRUEのところだけを返す
> mydata[mydata>3] [1] 3.4 3.4 3.7 3.7 > mydata>3 [1] FALSE TRUE TRUE TRUE TRUE FALSE FALSE FALSE FALSE FALSE
まだまだあるよ、アクセス方法
- 負の引数を取ると、そこを除いてベクトルにして返す
- []の中にc関数で負の値を入れておくと、複数個を取り除くこともできる
> mydata[-10] [1] 2.9 3.4 3.4 3.7 3.7 2.8 2.8 2.5 2.4 > mydata[-1] [1] 3.4 3.4 3.7 3.7 2.8 2.8 2.5 2.4 2.4 > mydata[c(-1,-2)] [1] 3.4 3.7 3.7 2.8 2.8 2.5 2.4 2.4
注意!!
- 難しくなってきたと思わないでね><
- すぐに身に付ける必要はない
- 「あ、こういうのあったな」と頭の中にインデックスを作ってもらうのが目的
- 「あったけど、どういう風に使うんだったっけ?」っていうときにまたここを開いてください♪
- というか、すぐにマスターされるとyoshid50がへこみます><
行列
- matrix関数
- ベクトルを行列に変換
- 列から順に決まっていく
> matrix(mydata,2,5) [,1] [,2] [,3] [,4] [,5] [1,] 2.9 3.4 3.7 2.8 2.4 [2,] 3.4 3.7 2.8 2.5 2.4
埋めていく順番
- byrow=Tをやると行から埋めていくことができるよ
> matrix(mydata,2,5,byrow=T) [,1] [,2] [,3] [,4] [,5] [1,] 2.9 3.4 3.4 3.7 3.7 [2,] 2.8 2.8 2.5 2.4 2.4
すでにあるベクトルを束ねる
- cbind
- rbind
> a<-c(1,2,3,4) > b<-c(5,6,7,8) > c<-c(9,10,11,12)
cbind
> cbind(a,b,c) a b c [1,] 1 5 9 [2,] 2 6 10 [3,] 3 7 11 [4,] 4 8 12
rbind
> rbind(a,b,c) [,1] [,2] [,3] [,4] a 1 2 3 4 b 5 6 7 8 c 9 10 11 12
行列へのアクセス方法
- これまた[]を使う
- 列ごと、行ごとの表示も可
- 「-」で取り除いたやつを返すのはベクトルのときと一緒
> d<-cbind(a,b,c) > d[2,3] [1] 10 > d[2,] a b c 2 6 10 > d[,3] [1] 9 10 11 12 > d[c(-2,-4),] a b c [1,] 1 5 9 [2,] 3 7 11
行列の基本演算
- 行列作って、足し算
- 直感的
> a<-matrix(c(1,2,3,4),2,2,byrow=T) > b<-matrix(c(1,2,3,4),2,2,byrow=T) > a+b [,1] [,2] [1,] 2 4 [2,] 6 8
積がやっかい
- 「**」にしちゃうと積にならないよ
> a**b [,1] [,2] [1,] 1 4 [2,] 9 16
積を求めたいときは「%**%」を使うべし
> a%**%b [,1] [,2] [1,] 7 10 [2,] 15 22
逆行列を求める
- solve関数
> solve(a) [,1] [,2] [1,] -2.0 1.0 [2,] 1.5 -0.5
ちなみに
- 単位行列になりました
- ゴミの範囲
> solve(a)%**%a [,1] [,2] [1,] 1.000000e-00 0 [2,] 1.110223e-16 1
行列式
- det関数
> det(a) [1] -2
行列演算系は
- R強いらしいです
- 早さ
- 分かりやすさ
配列
- 配列って何?
- おいしいの?
- ベクトルとは違うの?
ベクトルは2次元の配列
> matrix(1:9,3,3) [,1] [,2] [,3] [1,] 1 4 7 [2,] 2 5 8 [3,] 3 6 9 > is.array(matrix(1:9,3,3)) [1] TRUE
練習問題
- 1から100までの間で
- 1,5,9…
- 2,6,10…
- 3,7,11…
- 4,8,12…
- というベクトルを作ってください
- また、それらを列ごとにつないで行列にしてください
- 偶数を持つ列のみ表示してください
- 5分でやりましょう
解答
> a<-seq(1,100,by=4) > b<-seq(2,100,by=4) > c<-seq(3,100,by=4) > d<-seq(4,100,by=4) > e<-cbind(a,b,c,d) > head(e) a b c d [1,] 1 2 3 4 [2,] 5 6 7 8 [3,] 9 10 11 12 [4,] 13 14 15 16 [5,] 17 18 19 20 [6,] 21 22 23 24 > head(e[,c(-2,-4)]) a c [1,] 1 3 [2,] 5 7 [3,] 9 11 [4,] 13 15 [5,] 17 19 [6,] 21 23
一行で書けるよ
- matrix関数
> head(matrix(1:100,25,4,byrow=T)[,c(-2,-4)])
配列とは
- Rで配列と言ったら次元を限定せずに多次元配列と思っておいてください
- 3次元配列を作ってみる
> a<-array(1:24,c(2,4,3)) > a , , 1 [,1] [,2] [,3] [,4] [1,] 1 3 5 7 [2,] 2 4 6 8 , , 2 [,1] [,2] [,3] [,4] [1,] 9 11 13 15 [2,] 10 12 14 16 , , 3 [,1] [,2] [,3] [,4] [1,] 17 19 21 23 [2,] 18 20 22 24
配列へのアクセス
- 大体ベクトルのときと同じ
- 複雑になるので、配列自体を確認する癖をつけておいたほうがよい
> a[1,2,1] [1] 3
次元を調べる
- 行列 in 配列なので行列でもdimは使えるよ
- 2**4**3の配列ということ
> dim(a) [1] 2 4 3
リスト
- ベクトルや配列は似たようなデータ構造をまとめて束ねたようなもの
- リストは異なるデータ構造を束ねたもの
- いろんな種類のベクトルをまとめてもよし
- List in Listでも構わない
例
> list(c(1,2,3,4),"Yasuhisa Yoshida",matrix(1:4,2,2)) [[1]] [1] 1 2 3 4 [[2]] [1] "Yasuhisa Yoshida" [[3]] [,1] [,2] [1,] 1 3 [2,] 2 4
ちなみに
- リストではなくしてみると…
- ベクトルで返ってくる
> unlist(list(c(1,2,3,4),"Yasuhisa Yoshida",matrix(1:4,2,2))) [1] "1" "2" "3" "4" [5] "Yasuhisa Yoshida" "1" "2" "3" [9] "4"
リストへのアクセス
- ベクトルとはちょっと違う
- [[]]でアクセス
- []でもいいけど、返ってくる結果がリストになっていてちょっと複雑
- それ以降の要素についてはベクトルとかと同じ
> list<-list(c(1,2,3,4),"Yasuhisa Yoshida",matrix(1:4,2,2)) > list[[1]] [1] 1 2 3 4 > list[[2]] [1] "Yasuhisa Yoshida" > list[[3]] [,1] [,2] [1,] 1 3 [2,] 2 4 > list[[3]][1,] [1] 1 3
リストは結構難しい><
- 返ってきた結果が予想と違うこととかが結構ある
- 例:ベクトルだと思って処理しようとしたら、実はリストが返ってきててうまくいかない
- 対処法
- mode関数
- データ構造が何かを教えてくれる関数
例
- 1列目の1番目の値を取ってきたい
- うまくいかない。。。
- うまくいかない理由をmode関数で調べる
> list[1][1] $vec [1] 1 2 3 4 > list[[1]][1] [1] 1 > mode(list) [1] "list" > mode(list[[1]]) [1] "numeric" > mode(list[1]) [1] "list" >
リストの要素には名前を付けることができる
- 数字で覚えるのは面倒
- 名前でアクセスできるようにしよう
- 「$」でアクセスするよ
> list<-list(vec=c(1,2,3,4),name="Yasuhisa Yoshida",matrix=matrix(1:4,2,2)) > list $vec [1] 1 2 3 4 $name [1] "Yasuhisa Yoshida" $matrix [,1] [,2] [1,] 1 3 [2,] 2 4 > list$name [1] "Yasuhisa Yoshida" > list$matrix[2,2] [1] 4
データフレーム
- 見た目はほとんど行列と同じ
- 行と列に必ずラベルを持っていることが特徴
- 「$」でアクセスしたりするやつです
- 注意
- ベクトル構造は同じ長さ
- 行列構造は同じ行サイズ
- どうしてもそれでダメなら
- 配列
- リスト
- とかを使ってください
例
- とりあえずデータフレームにいれたいベクトルを用意
> ID1<-c(1,2,3,4,5) > VISIT1<-c(10,20,30,10,50) > SEX1<-c("F","M","M","F","F") > WEIGHT<-c(30,20,90,40,30)
データフレームを作る
- data.frame関数
> A<-data.frame(id=ID1,vit=VISIT1,sex=SEX1,w=WEIGHT) > A id vit sex w 1 1 10 F 30 2 2 20 M 20 3 3 30 M 90 4 4 10 F 40 5 5 50 F 30
データフレームに列を追加と削除
- 「$」付けてベクトルを代入
- 列を削除したいときにはNULLを代入
- cbindでもできる
- mergeという関数もある
> A$test<-c(1,2,3,4,5) > A id vit sex w test 1 1 10 F 30 1 2 2 20 M 20 2 3 3 30 M 90 3 4 4 10 F 40 4 5 5 50 F 30 5 > A$test<-NULL > A id vit sex w 1 1 10 F 30 2 2 20 M 20 3 3 30 M 90 4 4 10 F 40 5 5 50 F 30
データフレームに行を追加
- rbind
> rbind(A,c(2,20,"M",60)) id vit sex w 1 1 10 F 30 2 2 20 M 20 3 3 30 M 90 4 4 10 F 40 5 5 50 F 30 6 2 20 M 60
練習問題
- 以下のデータをファイルから読み込んで、データフレームにしてみましょう
- 列に("id","shako","sex","fn","ln")という名前を付けよう
- ファイルの頭に付けてもいいけど、今回はそうじゃないやり方でやってみよう
- できたら下のほうにあるコマンドを実行してね
- あとで説明する「因子型」っていうのが悪さしてしまうので
1 yoshid50 M yasuhisa yoshida 2 miyaga50 M hiroyuki miyagawa 3 ito50 M atushi ito 4 tantan50 F eri tantani
- やるコマンド
> shako$fn<-as.vector(shako$fn) > shako$ln<-as.vector(shako$ln) > shako$shako<-as.vector(shako$shako)
練習問題の続き
- 列にfullnameを付け加えよう
- 「yasuhisa yoshida」という風に連結されるようにしよう
- 文字列の連結はpaste関数でできるよ
paste(shako$fn,shako$ln,sep=" ")
完成予想図
- こんな感じを目指してください
> shako id shako sex fn ln fullname 1 1 yoshid50 M yasuhisa yoshida yasuhisa yoshida 2 2 miyaga50 M hiroyuki miyagawa hiroyuki miyagawa 3 3 ito50 M atushi ito atushi ito 4 4 tantan50 F eri tantani eri tantani
解答例
> shako<-read.table("shako.txt") > names(shako)<-c("id","shako","sex","fn","ln") > shako$fn<-as.vector(shako$fn) > shako$ln<-as.vector(shako$ln) > shako$shako<-as.vector(shako$shako) > shako$fullname<-paste(shako$fn,shako$ln,sep=" ") > shako[5,]<-c("5","onoue50","M","kentaro","onoue","kentaro onoue")
因子型
- yoshid50もこの前まで何のためにあるやつか分かっていなかった><
- でも、これを使えるようになると便利
- クロス分析
- ホワイトボードで説明
- マネイジメント実習でもやる…と思うよ
- 水野先生もこの前言ってたし
- 層別分析でも必要
- あとでやります
順序なし因子
- ベクトルを作る
- 規則性のある区間データに分ける
- 順序付けられてはいないよ
- 血液型とか職業とか
- 今回はたまたま
> a<-c(1,3,1,4,5,3,2,1,3,4,5,3,2,1,3,4,2) > cut(a,breaks=0:5) [1] (0,1] (2,3] (0,1] (3,4] (4,5] (2,3] (1,2] (0,1] (2,3] (3,4] (4,5] (2,3] [13] (1,2] (0,1] (2,3] (3,4] (1,2] Levels: (0,1] (1,2] (2,3] (3,4] (4,5] > b<-cut(a,breaks=0:5)
順序付ける
- ordered関数
- levels関数でlabelsをつけておく
> c<-ordered(a,labels=levels(b)) > c [1] (0,1] (2,3] (0,1] (3,4] (4,5] (2,3] (1,2] (0,1] (2,3] (3,4] (4,5] (2,3] [13] (1,2] (0,1] (2,3] (3,4] (1,2] Levels: (0,1] < (1,2] < (2,3] < (3,4] < (4,5] #変な変数いっぱい作るのが嫌いな人用ワンライナー > a<-ordered(a,labels=levels(cut(a,breaks=0:5)))
この辺で終わる予定
- 時間があれば先に進みます
これまで習ったデータ型の知識を使って層別分析にチャレンジ
- もうみんなこれくらはできるようになってるよ
irisのデータについて知ってみる
- あやめのデータ
- よく使われるデータ
- よい性質を持っているから
- 因子分析
- ?iris
irisの3番目のデータ持ってきて!!
- iris[3]でよい?
> iris[3] Petal.Length 1 1.4 2 1.4 3 1.3 4 1.5 5 1.4 6 1.7 7 1.4 8 1.5 9 1.4 10 1.5
- 3列目を持ってきてしまうorz
- 3行目が欲しい
どうするの?
- iris[3,]
- 3行目のデータ持ってきて
- 列は全部お願いね
> iris[3,] Sepal.Length Sepal.Width Petal.Length Petal.Width Species 3 4.7 3.2 1.3 0.2 setosa
- ex.「iris[3,2]」
> head(iris) Sepal.Length Sepal.Width Petal.Length Petal.Width Species 1 5.1 3.5 1.4 0.2 setosa 2 4.9 3.0 1.4 0.2 setosa 3 4.7 3.2 1.3 0.2 setosa 4 4.6 3.1 1.5 0.2 setosa 5 5.0 3.6 1.4 0.2 setosa 6 5.4 3.9 1.7 0.4 setosa
Sepal.Lengthの順に並び替えをしてみる
- order関数
- データが何番目にいるのかを返してくれる関数
> order(iris$Sepal.Length) [1] 14 9 39 43 42 4 7 23 48 3 30 12 13 25 31 46 2 10 [19] 35 38 58 107 5 8 26 27 36 41 44 50 61 94 1 18 20 22 [37] 24 40 45 47 99 28 29 33 60 49 6 11 17 21 32 85 34 37 [55] 54 81 82 90 91 65 67 70 89 95 122 16 19 56 80 96 97 100 [73] 114 15 68 83 93 102 115 143 62 71 150 63 79 84 86 120 139 64 [91] 72 74 92 128 135 69 98 127 149 57 73 88 101 104 124 134 137 147 [109] 52 75 112 116 129 133 138 55 105 111 117 148 59 76 66 78 87 109 [127] 125 141 145 146 77 113 144 53 121 140 142 51 103 110 126 130 108 131 [145] 106 118 119 123 136 132
並び替えをやってみる
> head(iris[order(iris$Sepal.Length),]) Sepal.Length Sepal.Width Petal.Length Petal.Width Species 14 4.3 3.0 1.1 0.1 setosa 9 4.4 2.9 1.4 0.2 setosa 39 4.4 3.0 1.3 0.2 setosa 43 4.4 3.2 1.3 0.2 setosa 42 4.5 2.3 1.3 0.3 setosa 4 4.6 3.1 1.5 0.2 setosa
二変数以上で並び替え
> head(iris[order(c(iris$Sepal.Length,iris$Sepal.Midth)),]) Sepal.Length Sepal.Width Petal.Length Petal.Width Species 14 4.3 3.0 1.1 0.1 setosa 9 4.4 2.9 1.4 0.2 setosa 39 4.4 3.0 1.3 0.2 setosa 43 4.4 3.2 1.3 0.2 setosa 42 4.5 2.3 1.3 0.3 setosa 4 4.6 3.1 1.5 0.2 setosa
irisデータ
- それぞれ50個ずついるよ
> summary(iris$Species) setosa versicolor virginica 50 50 50
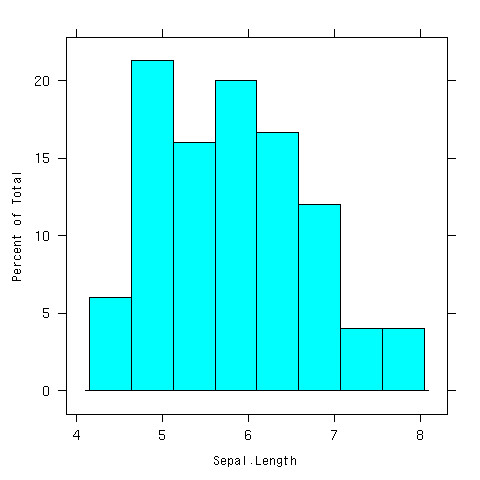
ヒストグラムを書いてみよう
> library(lattice) > histogram(~Sepal.Length,data=iris)
できあがり
- 普通のヒストグラムと一緒じゃん
- 違うよ、全然違うよ
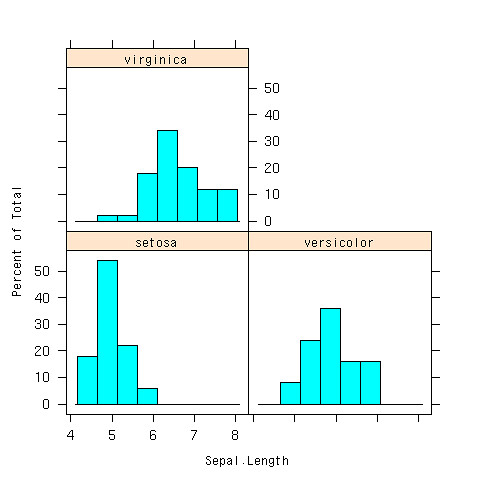
層別にヒスとグラムを書けるのがlatticeライブラリのhistgram
- 分布が違うね、とかいうことが分かる
> histogram(~Sepal.Length|Species,data=iris)
層別に統計量を出してくれるのがby関数
- 第一引数に求めたいデータ
- 第二引数に層別するもとのデータ
- 第三引数に求めたい統計量
- mean
- var
> by(iris$Sepal.Length,iris$Species,summary) INDICES: setosa Min. 1st Qu. Median Mean 3rd Qu. Max. 4.300 4.800 5.000 5.006 5.200 5.800 ------------------------------------------------------------ INDICES: versicolor Min. 1st Qu. Median Mean 3rd Qu. Max. 4.900 5.600 5.900 5.936 6.300 7.000 ------------------------------------------------------------ INDICES: virginica Min. 1st Qu. Median Mean 3rd Qu. Max. 4.900 6.225 6.500 6.588 6.900 7.900
行列やデータフレームを持ってくることもできる
- それぞれの列に対して層別された統計量を求める
> by(x[1:4],iris$Species,mean) iris$Species: setosa Sepal.Length Sepal.Width Petal.Length Petal.Width 5.006 3.428 1.462 0.246 ------------------------------------------------------------ iris$Species: versicolor Sepal.Length Sepal.Width Petal.Length Petal.Width 5.936 2.770 4.260 1.326 ------------------------------------------------------------ iris$Species: virginica Sepal.Length Sepal.Width Petal.Length Petal.Width 6.588 2.974 5.552 2.026
層別で頻度を集計する
- 条件を付けたりすることができる
> xtabs(~Species,data=iris,Sepal.Width>3) Species setosa versicolor virginica 42 8 17
散布図を層別で書いてみる
- 色分け
- 他にもいろいろオプションはあるよ
- ヘルプで見てね
> xyplot(Sepal.Length~Sepal.Width,data=iris,col=as.integer(iris$Species))
できあがり
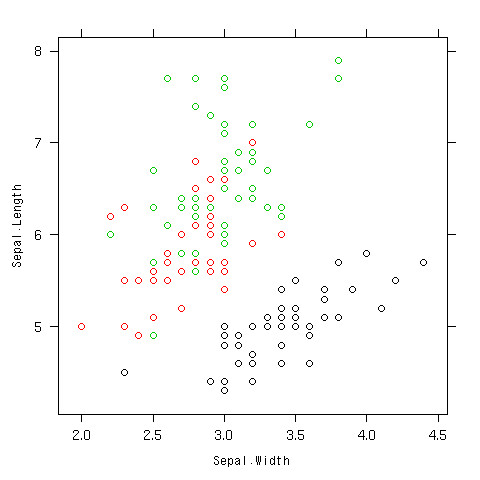
配布する資料が白黒だったら。。。
- そもそも散布図を3つ書けばよい
- 「|」の後に因子データを持ってくる
> xyplot(Sepal.Length~Sepal.Width|Species,data=iris)
できあがり
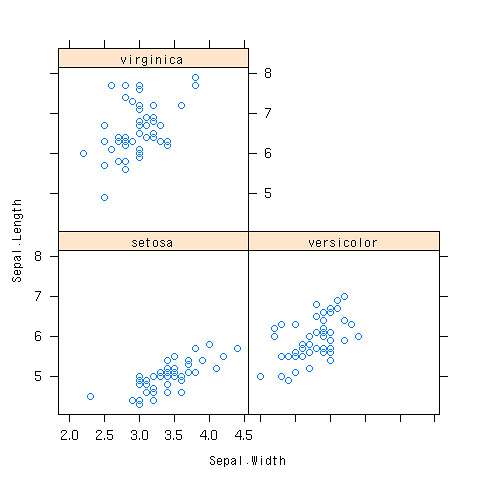
irisのデータで相関係数行列を求めよう
- 前回やってる
- 5列目は因子だから要らない
> cor(iris[1:4]) Sepal.Length Sepal.Width Petal.Length Petal.Width Sepal.Length 1.0000000 -0.1175698 0.8717538 0.8179411 Sepal.Width -0.1175698 1.0000000 -0.4284401 -0.3661259 Petal.Length 0.8717538 -0.4284401 1.0000000 0.9628654 Petal.Width 0.8179411 -0.3661259 0.9628654 1.0000000
別解
- 「[-5]」と書くと5列目を抜いた行列を返してくれるよ
> cor(iris[-5]) Sepal.Length Sepal.Width Petal.Length Petal.Width Sepal.Length 1.0000000 -0.1175698 0.8717538 0.8179411 Sepal.Width -0.1175698 1.0000000 -0.4284401 -0.3661259 Petal.Length 0.8717538 -0.4284401 1.0000000 0.9628654 Petal.Width 0.8179411 -0.3661259 0.9628654 1.0000000
相関係数行列の問題
- 数字が多くて分かりづらい
- 例:10×10の相関係数行列
- どこが相関係数が大きいか知りたい
- グラフィックに表そう
相関係数行列の見た目を変える
- symnum関数
> symnum(abs(cor(iris[-5])),cutpoint=c(0,0.2,0.4,0.6,0.8,1),symbols=c(" ",".","-","+","**")) S.L S.W P.L P.W Sepal.Length ** ** ** Sepal.Width ** - . Petal.Length ** - ** ** Petal.Width ** . ** ** attr(,"legend") [1] 0 ' ' 0.2 '.' 0.4 '-' 0.6 '+' 0.8 '**' 1
symnum関数は便利!!
- 数値データを区間データに分ける
- 例えば、クロス分析
- 数字が都道府県と対応
- 関東地方とかで分ける
- プログラムでも書けるけど、それだけのために書くのって結構面倒
- Rでできないの?
- できます!!
symnum関数で数値データを区間データに分ける
> symnum(iris$Sepal.Length,cutpoint=c(4,4.5,5,5.5,6,6.5,7,7.5,8),symbols=c("4.0~4.5","4.5~5","5~.5.5","5.5~6","6~6.5","6.5~7","7~7.5","7.5~8")) [1] 5~.5.5 4.5~5 4.5~5 4.5~5 4.5~5 5~.5.5 4.5~5 4.5~5 4.0~4.5 [10] 4.5~5 5~.5.5 4.5~5 4.5~5 4.0~4.5 5.5~6 5.5~6 5~.5.5 5~.5.5 [19] 5.5~6 5~.5.5 5~.5.5 5~.5.5 4.5~5 5~.5.5 4.5~5 4.5~5 4.5~5 [28] 5~.5.5 5~.5.5 4.5~5 4.5~5 5~.5.5 5~.5.5 5~.5.5 4.5~5 4.5~5 [37] 5~.5.5 4.5~5 4.0~4.5 5~.5.5 4.5~5 4.0~4.5 4.0~4.5 4.5~5 5~.5.5 [46] 4.5~5 5~.5.5 4.5~5 5~.5.5 4.5~5 6.5~7 6~6.5 6.5~7 5~.5.5 [55] 6~6.5 5.5~6 6~6.5 4.5~5 6.5~7 5~.5.5 4.5~5 5.5~6 5.5~6 [64] 6~6.5 5.5~6 6.5~7 5.5~6 5.5~6 6~6.5 5.5~6 5.5~6 6~6.5 [73] 6~6.5 6~6.5 6~6.5 6.5~7 6.5~7 6.5~7 5.5~6 5.5~6 5~.5.5 [82] 5~.5.5 5.5~6 5.5~6 5~.5.5 5.5~6 6.5~7 6~6.5 5.5~6 5~.5.5 [91] 5~.5.5 6~6.5 5.5~6 4.5~5 5.5~6 5.5~6 5.5~6 6~6.5 5~.5.5 [100] 5.5~6 6~6.5 5.5~6 7~7.5 6~6.5 6~6.5 7.5~8 4.5~5 7~7.5 [109] 6.5~7 7~7.5 6~6.5 6~6.5 6.5~7 5.5~6 5.5~6 6~6.5 6~6.5 [118] 7.5~8 7.5~8 5.5~6 6.5~7 5.5~6 7.5~8 6~6.5 6.5~7 7~7.5 [127] 6~6.5 6~6.5 6~6.5 7~7.5 7~7.5 7.5~8 6~6.5 6~6.5 6~6.5 [136] 7.5~8 6~6.5 6~6.5 5.5~6 6.5~7 6.5~7 6.5~7 5.5~6 6.5~7 [145] 6.5~7 6.5~7 6~6.5 6~6.5 6~6.5 5.5~6 attr(,"legend") [1] 4 '4.0~4.5' 4.5 '4.5~5' 5 '5~.5.5' 5.5 '5.5~6' 6 '6~6.5' 6.5 '6.5~7' 7 '7~7.5' 7.5 '7.5~8' 8
元のデータはこれ
- さっきのと対応させてみてね
- 以下、未満などなど
> iris$Sepal.Length [1] 5.1 4.9 4.7 4.6 5.0 5.4 4.6 5.0 4.4 4.9 5.4 4.8 4.8 4.3 5.8 5.7 5.4 5.1 [19] 5.7 5.1 5.4 5.1 4.6 5.1 4.8 5.0 5.0 5.2 5.2 4.7 4.8 5.4 5.2 5.5 4.9 5.0 [37] 5.5 4.9 4.4 5.1 5.0 4.5 4.4 5.0 5.1 4.8 5.1 4.6 5.3 5.0 7.0 6.4 6.9 5.5 [55] 6.5 5.7 6.3 4.9 6.6 5.2 5.0 5.9 6.0 6.1 5.6 6.7 5.6 5.8 6.2 5.6 5.9 6.1 [73] 6.3 6.1 6.4 6.6 6.8 6.7 6.0 5.7 5.5 5.5 5.8 6.0 5.4 6.0 6.7 6.3 5.6 5.5 [91] 5.5 6.1 5.8 5.0 5.6 5.7 5.7 6.2 5.1 5.7 6.3 5.8 7.1 6.3 6.5 7.6 4.9 7.3 [109] 6.7 7.2 6.5 6.4 6.8 5.7 5.8 6.4 6.5 7.7 7.7 6.0 6.9 5.6 7.7 6.3 6.7 7.2 [127] 6.2 6.1 6.4 7.2 7.4 7.9 6.4 6.3 6.1 7.7 6.3 6.4 6.0 6.9 6.7 6.9 5.8 6.8 [145] 6.7 6.7 6.3 6.5 6.2 5.9
symnum関数の戻り値を見てみる
- mode関数はオブジェクトが何者かを示す
- listとかarrayという具合に教えてくれる
- 今回はキャラクター型らしい
> kukan<-symnum(iris$Sepal.Length,cutpoint=c(4,4.5,5,5.5,6,6.5,7,7.5,8),symbols=c("4.0~4.5","4.5~5","5~.5.5","5.5~6","6~6.5","6.5~7","7~7.5","7.5~8")) > mode(kukan) [1] "character"
因子型
- 層別分析をするために必要なデータの型はfactor(因子)型
- キャラクター型から因子型への変換
- これをirisのデータにくっつけるなりをすれば層別分析ができるようになる
> factor(kukan) [1] 5~.5.5 4.5~5 4.5~5 4.5~5 4.5~5 5~.5.5 4.5~5 4.5~5 4.0~4.5 [10] 4.5~5 5~.5.5 4.5~5 4.5~5 4.0~4.5 5.5~6 5.5~6 5~.5.5 5~.5.5 [19] 5.5~6 5~.5.5 5~.5.5 5~.5.5 4.5~5 5~.5.5 4.5~5 4.5~5 4.5~5 [28] 5~.5.5 5~.5.5 4.5~5 4.5~5 5~.5.5 5~.5.5 5~.5.5 4.5~5 4.5~5 [37] 5~.5.5 4.5~5 4.0~4.5 5~.5.5 4.5~5 4.0~4.5 4.0~4.5 4.5~5 5~.5.5 [46] 4.5~5 5~.5.5 4.5~5 5~.5.5 4.5~5 6.5~7 6~6.5 6.5~7 5~.5.5 [55] 6~6.5 5.5~6 6~6.5 4.5~5 6.5~7 5~.5.5 4.5~5 5.5~6 5.5~6 [64] 6~6.5 5.5~6 6.5~7 5.5~6 5.5~6 6~6.5 5.5~6 5.5~6 6~6.5 [73] 6~6.5 6~6.5 6~6.5 6.5~7 6.5~7 6.5~7 5.5~6 5.5~6 5~.5.5 [82] 5~.5.5 5.5~6 5.5~6 5~.5.5 5.5~6 6.5~7 6~6.5 5.5~6 5~.5.5 [91] 5~.5.5 6~6.5 5.5~6 4.5~5 5.5~6 5.5~6 5.5~6 6~6.5 5~.5.5 [100] 5.5~6 6~6.5 5.5~6 7~7.5 6~6.5 6~6.5 7.5~8 4.5~5 7~7.5 [109] 6.5~7 7~7.5 6~6.5 6~6.5 6.5~7 5.5~6 5.5~6 6~6.5 6~6.5 [118] 7.5~8 7.5~8 5.5~6 6.5~7 5.5~6 7.5~8 6~6.5 6.5~7 7~7.5 [127] 6~6.5 6~6.5 6~6.5 7~7.5 7~7.5 7.5~8 6~6.5 6~6.5 6~6.5 [136] 7.5~8 6~6.5 6~6.5 5.5~6 6.5~7 6.5~7 6.5~7 5.5~6 6.5~7 [145] 6.5~7 6.5~7 6~6.5 6~6.5 6~6.5 5.5~6 Levels: 4.0~4.5 4.5~5 5.5~6 5~.5.5 6.5~7 6~6.5 7.5~8 7~7.5
おみやげ
- データ
- Rリンク集
- 使ってね
次回予告
- グラフィック特集
- 計算を早くする関数と層別分析
- データ解析特集
- 数理統計学
- 因子分析
- クラスター分析
- 品質管理
- QCの7つ道具
- 時系列分析
どれがやりたいですか?
- 多数決取ります
参考書籍1

- 作者: 熊谷悦生,舟尾暢男
- 出版社/メーカー: 九天社
- 発売日: 2007/04
- メディア: 単行本
- 購入: 1人 クリック: 19回
- この商品を含むブログ (14件) を見る
参考書籍2

The R Tips―データ解析環境Rの基本技・グラフィックス活用集
- 作者: 舟尾暢男
- 出版社/メーカー: 九天社
- 発売日: 2005/02
- メディア: 単行本
- 購入: 3人 クリック: 20回
- この商品を含むブログ (34件) を見る