3章で扱ったのは経験的分位点分位点プロット、すなわちあるデータとデータの分布が等しいものだった。しかし、論理的分位点分位点プロットはそうではない。実際のデータがある理論的な分布に従うかどうかを調べるものである。具体的には標準正規分布に従うかどうか、などを調べるときに調べる。
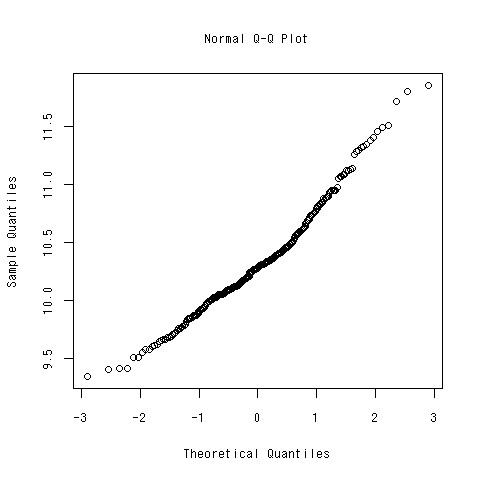
実際のデータが完全に標準正規分布に従っているのなら、理論的分位点分位点プロットはy=xのような形になるが、そうなることはまずない。しかし、実際のデータが正規分布にみなせる場合に共通することは、理論的分位点分位点プロットが直線になるということである。平均が違うのなら、切片が異なる、分散が異なるのなら傾きが異なる(正確には標準偏差倍変わる)。しかし、どの場合も正規分布に従うのならば、直線の形であるということが分かる。直線の形になっていれば、正規分布に従うといえ、回帰分析のようなことができるようになる。
実際のデータがそのまま正規分布に従うということは、まず考えられない。そこで変換をすることが必要になるが、それは前にやったlogで変換したり、平方根を取ったりするなどをやればよい。
理論的分位点分位点プロットの実際のやり方は以下のようにやればよい。
qqnorm(rainfall)
この図を書いたあとにablineを使って、直線とみなすことができるかどうかを見ていけばよい。できあがりの図は以下のような感じ。