ベイズの事後分布と事後予測分布を出してみた

MCMCで、って言ったそばからあれなんですが、研究室の先輩と話してたらできそうだ、ということでやりました。できました。

事後分布について

コインを二回投げて、表なら1、裏なら0でその和について考える。この和の事前分布をとりあえず一様分布*1としておく。この場合のパラメータの事後分布は一般に次のように書けるはず*2。
$f(\theta | y_1,\cdots,y_n)=\frac{\theta^{\sum_{i=1}^{n}y_i}(1-\theta)^{2n-\sum_{i=1}^{n}y_i}}{\beta(\sum_{i=1}^{n}y_i+1,2n+1-\sum_{i=1}^{n}y_i)}\{\theta:0<\theta<1\}$
で、これがデータが与えられるにつれて、どのように変化していくか、というのを見ようということをやりたかったのである。

ひとまずindicator functionとposterior distributionをRで以下のように定義する。関数を返す関数になっているが、尤度関数でパラメータを求めさせたことがある人とかなら普通にやったことがあるようなやつである。

indicator_function<- function(x){
  if(0 <= all(x) & all(x) <= 1){
    return(1)
  }else{
    return(0)
  }
}

posterior_distribution_function <- function(x){
  return(
         function(theta){
           theta^(sum(x)) * (1-theta)^((length(x)*2)-sum(x)) / beta(1+sum(x),1+2*length(x)-sum(x)) * indicator_function(theta)
         }
         )
}

で、これを使って色々やってみる。2回のコイントスの試行の回数を変化させてみる。

par(mfrow=c(c(5,2)))
for(i in 1:10){
  plot(posterior_distribution_function(rep(c(0),i*10)),0,1,xlim=c(0,0.2),main=paste("i=",i*10,"の場合",sep=""))
}

すると分布は次のような変化をしていく。

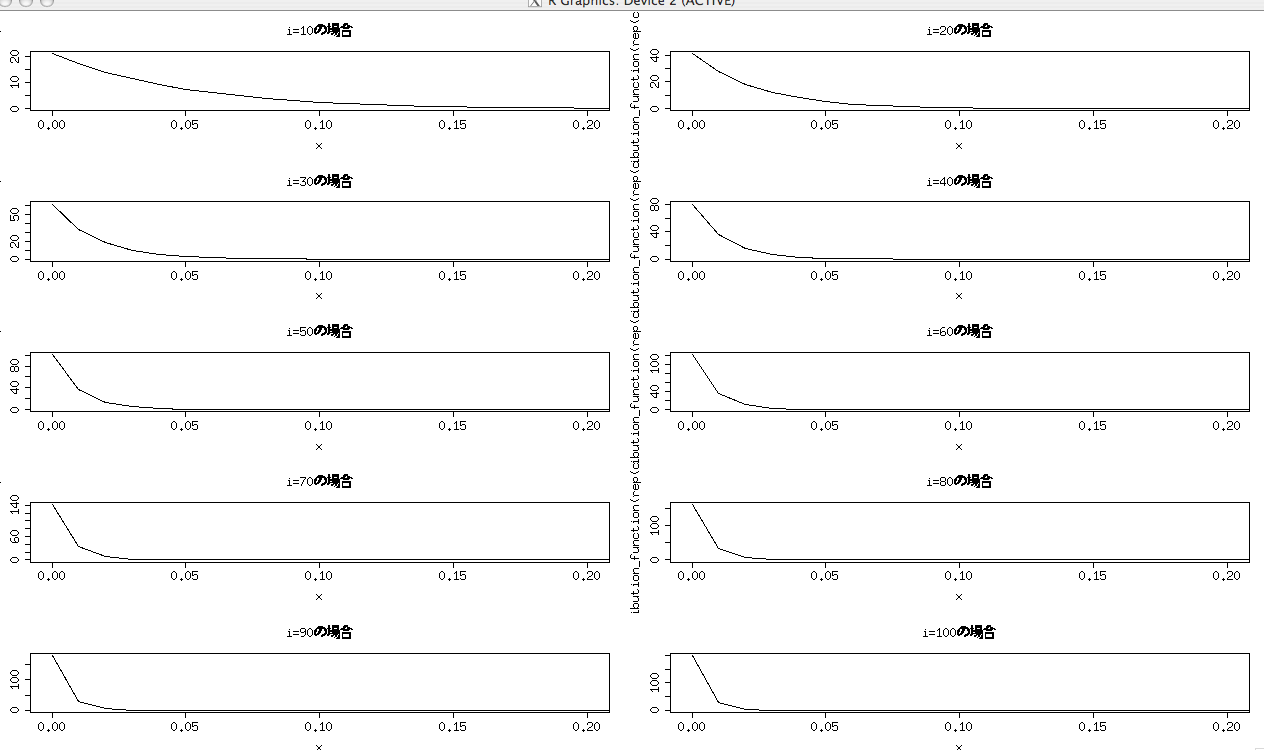
ずっと0ばっかり出ているから0の出る確率がどんどん高くなっていくのが分かる。

次に表の出るのが0、1、2という等確率だとどうなるかを見ていく。

par(mfrow=c(c(5,2)))
for(i in 1:10){
  plot(posterior_distribution_function(rep(c(0,1,2),10*i)),0,1,xlim=c(0.4,0.6),main=paste("i=",i*10,"の場合",sep=""))
}

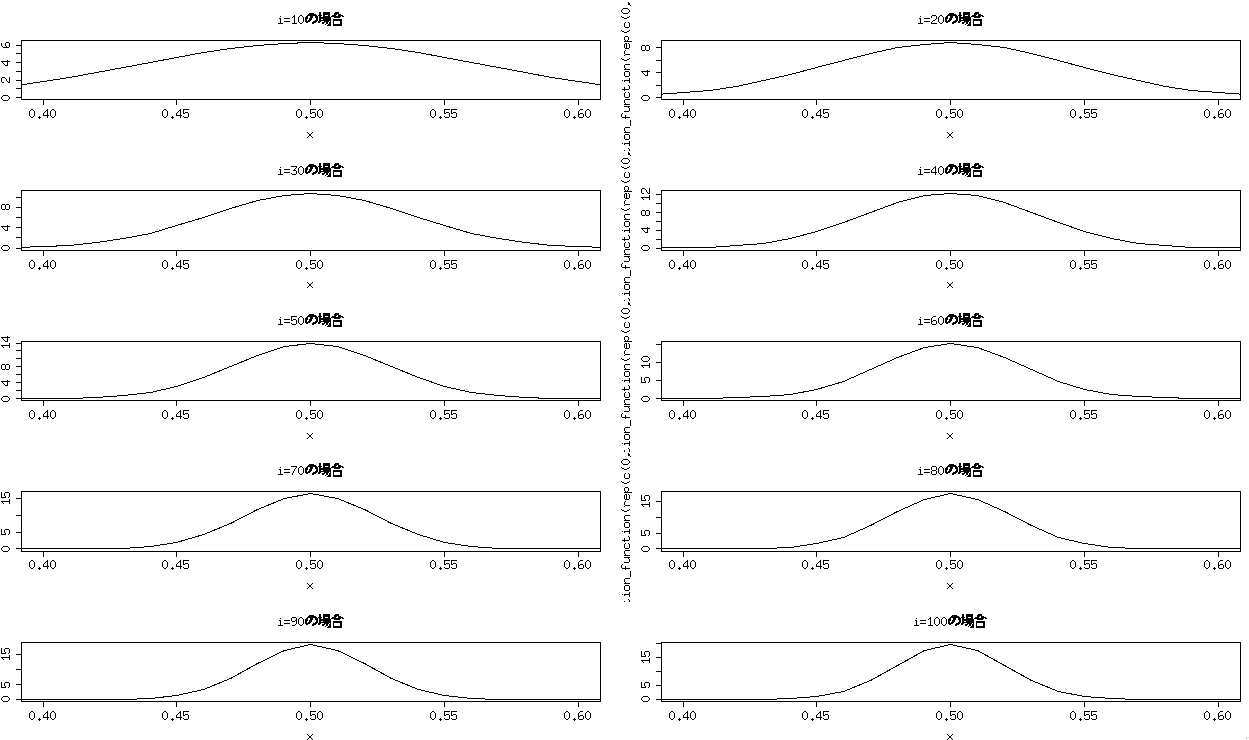
もちろん等確率なので、0.5になるのは分かっているんだけど、分散が小さくなっていくのが分かるかと思う。これはベイズの時だけど、頻度論の時はこの辺にあるので、参考になる…かもしれない。

事後分布が分かったので、事後予測分布も計算することができる。そのための関数を以下のように定義する。

predictive_posterior_distribution_function <- function(x){
  return(
         function(x_n){
           choose(2,x_n) * beta(1+sum(x)+x_n,3+2*length(x)-(sum(x)+x_n)) / beta(1+sum(x),1+2*length(x)-sum(x))
         }
         )
}

例えば、一回目と二回目の試行での和がそれぞれ0だったとする時、三回目の試行で0、1、2が出る確率は次のように計算できる。

> predictive_posterior_distribution_function(c(0,0))(0)
[1] 0.7142857
> predictive_posterior_distribution_function(c(0,0))(1)
[1] 0.2380952
> predictive_posterior_distribution_function(c(0,0))(2)
[1] 0.04761905

こいつの分布をプロットすることもできるのだが、Rは階乗の計算をガンマ関数で計算しているらしく、非整数の時も計算できてしまうためプロットすると変になってしまう*3。まあ、整数の時の値はちゃんと計算できている。

これから

この例では、積分の計算がベータ関数にうまいこと置きかえられたので、うまいこと事後分布を計算することができたが、一般の場合でうまくいくとは到底思えない。というかいかない。まあ、うまくいったとしても、事前分布ごとに事後分布の形状がどうなるかとかを計算してやんないといけないっぽいので、これはとてもめんどい。とまあそんなこんな理由でMCMCが使われているんだろう。