習ったついでに遊んでみるテスト。この前ここで定常時系列データを作ったが、あれはARモデルに沿って作ったようなやり方になっているらしい。で、今日は時系列分析における相関係数、自己相関係数を習ったのでそれを使ってみる。
定常時系列データを作る関数。再掲。パラメータと作るデータセットの数を指定(指定しなくてもいいけど)。
teijyou<-function(b=0.5,n=100){ x<-rnorm(1) for(i in 2:n){ x[i]<-b*x[i-1]+rnorm(1) } return(x) }
標本自己共分散はで、標本自己相関係数は
であるが、わざわざ自分で作らなくてもRにはこれを求める関数が用意されている。ちなみにさっきのteijyouとかいう関数もRのarとかいうのを使えば不要な気がするけど、まあいいや。先週せっかく作ったし。
自己共分散、自己相関係数を求める関数はacfという関数である。acf(x,type="",plot=TRUE,...)という具合になっていて、typeはディフォルトは自己相関係数を求めるようになっている。自己共分散が欲しいときにはtypeにcovarianceと指定してやればよい。plot=FALSEを指定すればプロットせずにプロットするためにどういうデータが使われているかとかを見ることができる。例にプロットしてみたのが次の画像。
> acf(teijyou(b=0.9,n=1000))
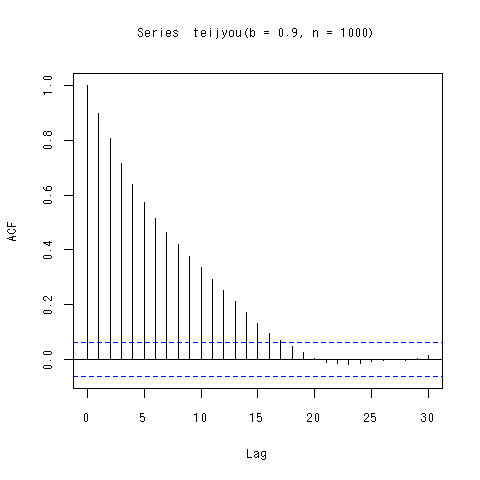
低減していく感じが見て取れますね。
> acf(teijyou(b=-0.9,n=1000))
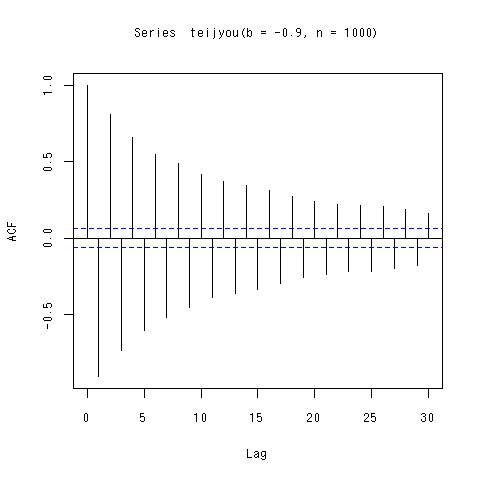
パラメータを負にすると授業中にもやっていたように「+,-+,-」を交互にやっていくような感じで。
これまでのデータは定常時系列データだったわけだけど、例に周期制のあるデータだと自己係数がどうなるかを見てみよう。今回はUKgasというデータを使用する。UKgasというのは「?UKgas」やってもらえば分かるのだが、1960年から1986年までのイギリスのガスの消費量を四半期ごとに観測した時系列のデータのことであります。周期制を持っているっていうのはプロットしてみると余計に分かりやすくなる。
> plot(UKgas)
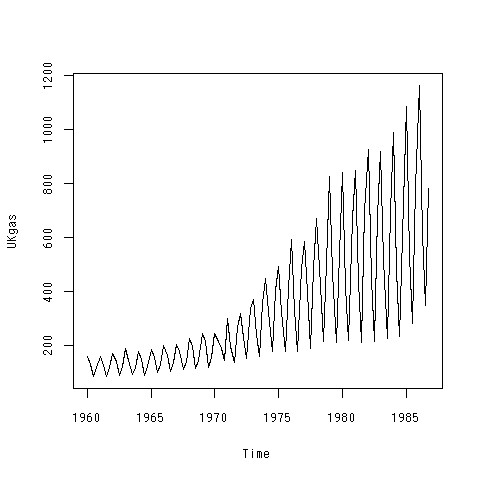
これでさっきのacfを使ってみると
> acf(UKgas)
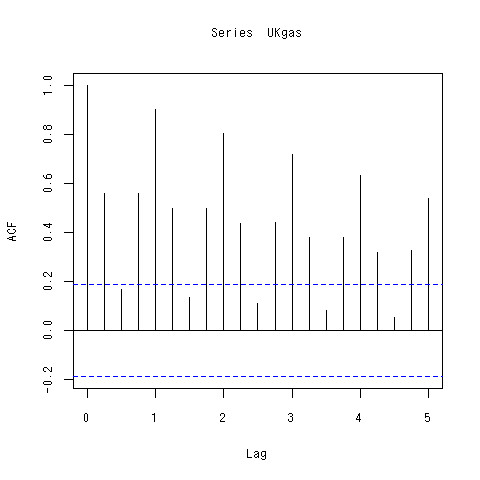
自己相関係数にも周期があることが分かりますね。それぞれ低減はしているようですが。なるほど、実験的な感じだけど、時系列分析において自己相関係数を見ることは意味があるんだなと分かったことが今日の収穫。
あと、時系列分析に限らないけど、以下のサイトがめちゃくちゃ分かりやすい。R使う人は読まないと人生損します。

経済・ファイナンスデータの計量時系列分析 (統計ライブラリー)
- 作者: 沖本竜義
- 出版社/メーカー: 朝倉書店
- 発売日: 2010/02/01
- メディア: 単行本
- 購入: 4人 クリック: 101回
- この商品を含むブログ (6件) を見る