これを見てたらn-gramは聞いたことしかないんだけど、embedという関数が出てきた。rubyのeach_consと似たような感じらしい*1。具体的にはこういうのね。
> embed(1:10,3) [,1] [,2] [,3] [1,] 3 2 1 [2,] 4 3 2 [3,] 5 4 3 [4,] 6 5 4 [5,] 7 6 5 [6,] 8 7 6 [7,] 9 8 7 [8,] 10 9 8
何か実験してみることにする。例えば1:100まで生成して、それをsinで変換したオブジェクトをxとかにする。
x <- sin(seq(0,2*pi,length=100))
それをplotしてやると見なれたものが出てくる。
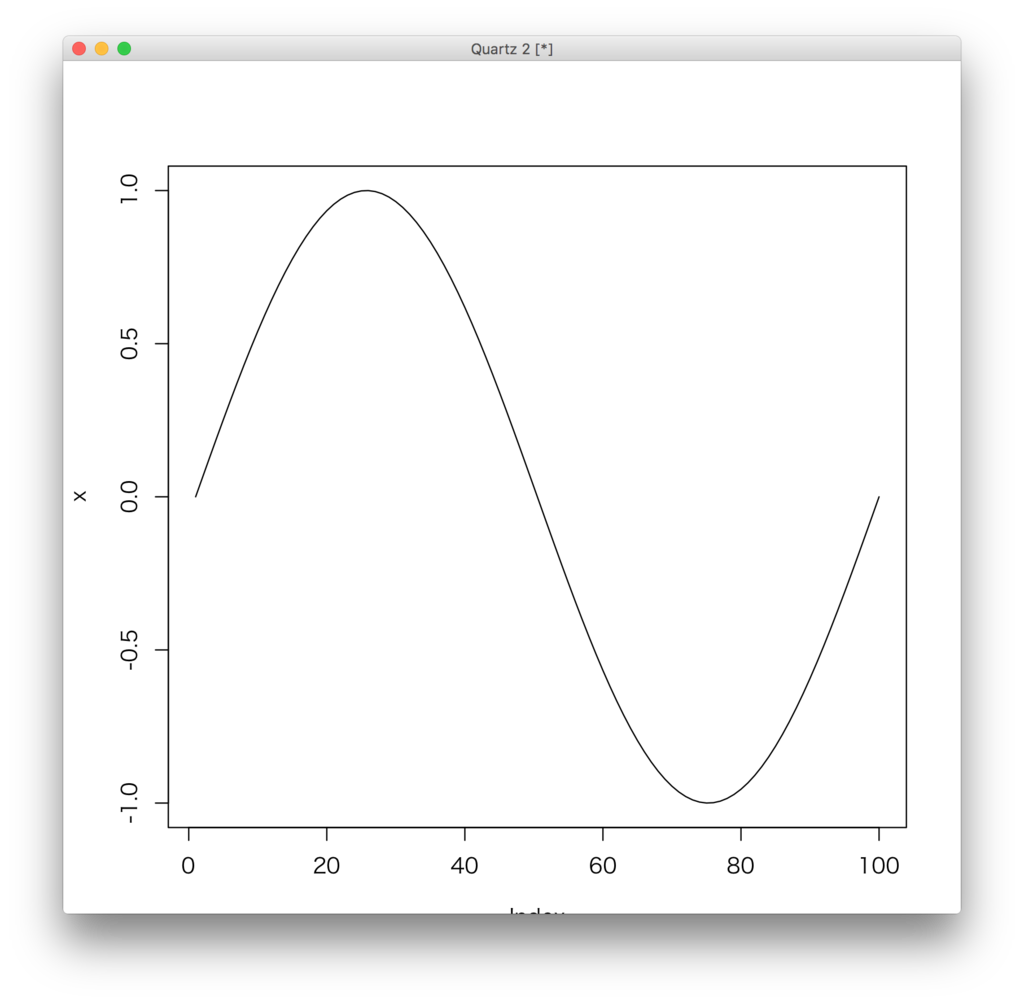
これに平均0で、標準偏差0.3の正規乱数を加えてやる。
x <- x+rnorm(x,sd=0.3)
これがどんなものかplotしてみる。
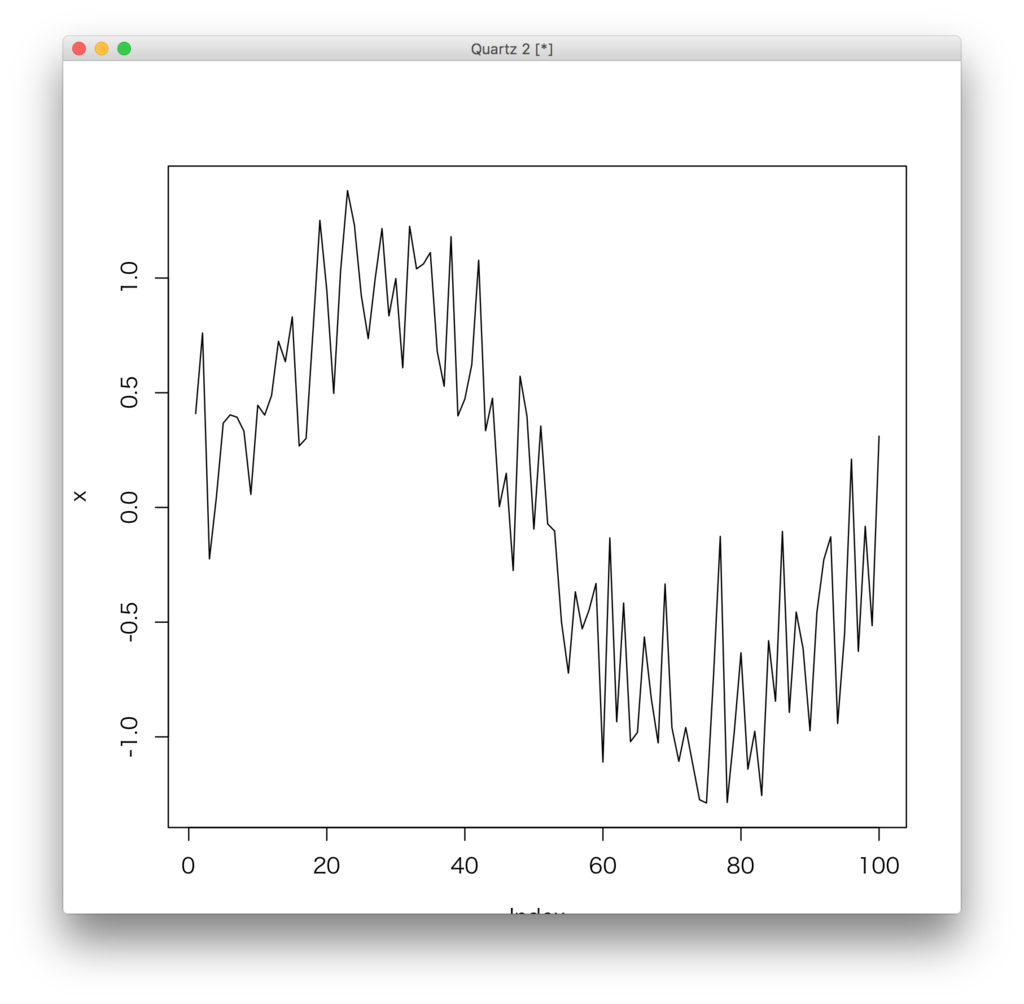
もとの特徴がちょっと分からなくなってしまった感じがある。で、xがsinから生成されているとか一旦忘れる。xは何でもいいんだけど、例えば株価のデータだとする。で、この株価が大体どんな変動をしているのかとかを知りたい。
特徴を知るために、例えば3期の平均を次々に取ることにする。3期の平均を取ればちょっとノイズに負けないで、特徴をつかめるんじゃない?的な考え。で、以下が3期ごとで平均を取ったもの。
apply(apply(embed(seq_along(x),3), 1, function(i) x[i]),2,mean)
で、これをplotするとこうなる。大分特徴がつかみやすくなったんじゃないか?*2
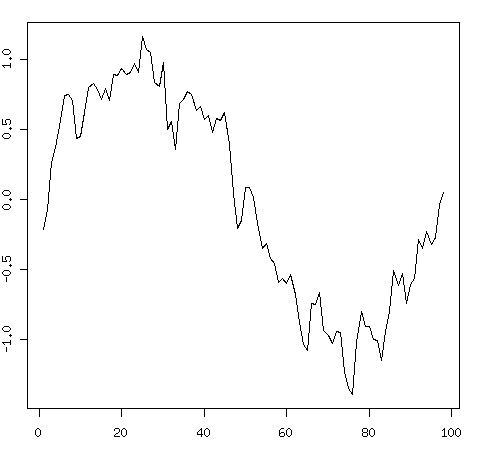
平均と取るってことはデータに均一に重みを付けているわけで、「最近のほど重みを増やすべきじゃない?」とか「周期性みたいなのがあったら、重みの付けかたも工夫しないといけないんじゃない?」とかって考えが出てくるかもしれないんだけど、それは時系列のarima,sarimaな考えにつながっていく。
まあ、大体の特徴つかみてーみたいな時はこんなのでおkということですね。簡単簡単。
ちなみに
Rでは平滑化も簡単にできるので、平滑化したらどうなるかを調べてみた。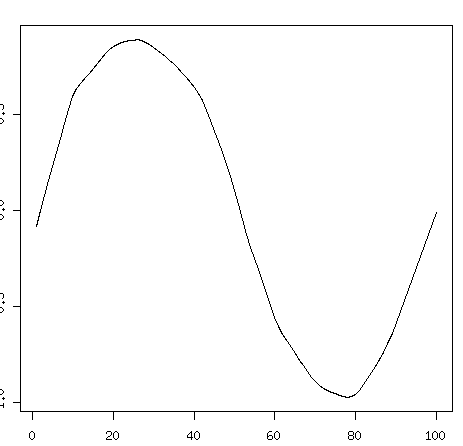
これだと元がsinってもろ分かりですね。もとのデータと重ねてみる。
plot(x,type="l") lines(lowess(seq_along(x),x,f=.2),col="red")
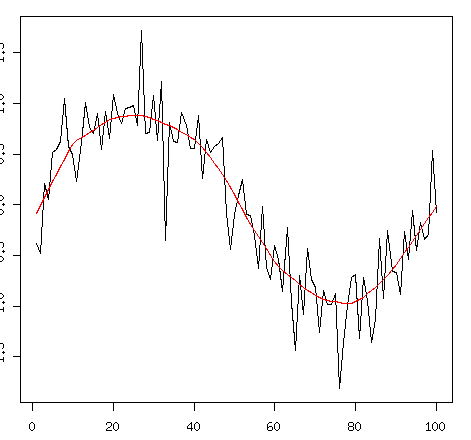
平滑化についてきちんとアグゴリズムというか計算の過程を勉強したわけではないんだけど、大体のエッセンス的なところはデータ解析でやったりした。大体知りたいんだったら参考になる…かもしれない。