Rの基本データ構造、よく使う関数紹介

Agenda
データ構造
- たくさんある＞＜
ベクトル
Rの格言
- いろんなベクトルの作り方
- 規則的データの生成
- 同じデータを繰り返す
- ベクトルへのアクセスの方法
- アクセス方法にもいろいろある
- まだまだあるよ、アクセス方法
行列
- 埋めていく順番
- すでにあるベクトルを束ねる
  - cbind
  - rbind
- 行列へのアクセス方法
- 行列の基本演算
  - 積がやっかい
  - 積を求めたいときは「%*%」を使うべし
- 逆行列を求める
  - ちなみに
- 行列式
- 固有値
配列
リスト
- 例
- ちなみに
- unlistのtips
- リストへのアクセス
  - リストは結構難しい＞＜
  - 例
- リストの要素には名前を付けることができる
- Rでlistがどのように使われているか
データフレーム
- 例
- データフレームを作る
- データフレームに列を追加と削除
- データフレームに行を追加
因子型
- irisのデータでやってみる
- irisデータ
  - 層別にSepal.Lengthの長さを調べてみる
  - ヒストグラムを書いてみよう
できあがり
- 層別にヒスとグラムを書けるのがlatticeライブラリのhistgram
- 層別に統計量を出してくれるのがby関数
- 行列やデータフレームを持ってくることもできる
- 層別で頻度を集計する
- 散布図を層別で書いてみる
  - できあがり
- 配布する資料が白黒だったら。。。
  - できあがり
- irisのデータで相関係数行列を求めよう
  - 別解
- 相関係数には注意が必要
- 線形じゃないけど、明らかに関係がある例
データ構造編
関数編
データ解析の時によく使う関数
sumamry関数
- 例えばデータフレーム
- 例えばリストに対して
- 例えばlmオブジェクト(回帰分析の結果)に対して
- 裏ではsummary関数が頑張っている
plot関数
- 1変数のデータに対して
- 2変数のデータに対して
- 時系列データに対して
- 裏ではplotが(ry
総称的関数のいいところ
str関数
- 例えばリストの構造を見るとか
- 例えばlmオブジェクトからp-valueのみを取り出したい時とか
やっていく過程
- head関数
(データ解析だけに限らない)関数
関数定義
- ディフォルト値
  - 例
  - 無名関数も、もちろんできる
Rにおける無名関数の使いどころは?

Agenda

Rのデータ構造、知ってると便利な関数とかを紹介
文法っぽいところはできるだけ話さないで、"Rらしい"ところを説明する予定

データ構造

ベクトル
行列
配列
リスト
データフレーム
因子

たくさんある＞＜

Rらしい(と思う)のは
- リスト
- データフレーム
- 因子

ベクトル

mydata <- c(1,2,3,4,5,6,7,8,9,10)

Rの格言

「意味のあるときは常に、意味の無いときも常にベクトル化を心がけよ」

いろんなベクトルの作り方

自分の手で打つのが面倒なやつとか
乱数をベクトルにするとか

規則的データの生成

Rubyの1..10みたいな
seq関数
第一引数から第二引数まで
byの間隔で数列を作る

> 1:10
 [1]  1  2  3  4  5  6  7  8  9 10
> seq(1,2,by=0.1)
 [1] 1.0 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.9 2.0

同じデータを繰り返す

rep関数
第一引数のデータを
times回繰り返す

> rep(c("a","b","c"),times=10)
 [1] "a" "b" "c" "a" "b" "c" "a" "b" "c" "a" "b" "c" "a" "b" "c" "a" "b" "c" "a"
[20] "b" "c" "a" "b" "c" "a" "b" "c" "a" "b" "c"

ベクトルへのアクセスの方法

[]
シーケンスを投げると、そこの部分をベクトルにして返してくれる

> mydata
 [1]  1  2  3  4  5  6  7  8  9 10
> mydata[5]
[1] 5
> mydata[3:5]
[1] 3 4 5

アクセス方法にもいろいろある

論理値でTRUEのところだけを返す

> mydata[mydata > 3]
[1]  4  5  6  7  8  9 10
> mydata > 3
 [1] FALSE FALSE FALSE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE

まだまだあるよ、アクセス方法

負の引数を取ると、そこを除いてベクトルにして返す
- 末尾のほうを見る言語に慣れている人はややこしく感じるところかも
[]の中にc関数で負の値を入れておくと、複数個を取り除くこともできる

> mydata[-10]
[1] 1 2 3 4 5 6 7 8 9
> mydata[-1]
[1]  2  3  4  5  6  7  8  9 10
> mydata[c(-1,-2)]
[1]  3  4  5  6  7  8  9 10

行列

matrix関数
ベクトルを行列に変換
列から順に決まっていく

> matrix(mydata,2,5)
     [,1] [,2] [,3] [,4] [,5]
[1,]    1    3    5    7    9
[2,]    2    4    6    8   10

埋めていく順番

byrow=Tをやると行から埋めていくことができるよ

> matrix(mydata,2,5,byrow=T)
     [,1] [,2] [,3] [,4] [,5]
[1,]    1    2    3    4    5
[2,]    6    7    8    9   10

すでにあるベクトルを束ねる

cbind
rbind

> a <- c(1,2,3,4)
> b <- c(5,6,7,8)
> c <- c(9,10,11,12)

cbind

> cbind(a,b,c)
     a b  c
[1,] 1 5  9
[2,] 2 6 10
[3,] 3 7 11
[4,] 4 8 12

rbind

> rbind(a,b,c)
  [,1] [,2] [,3] [,4]
a    1    2    3    4
b    5    6    7    8
c    9   10   11   12

行列へのアクセス方法

これまた[]を使う
列ごと、行ごとの表示も可
「-」で取り除いたやつを返すのはベクトルのときと一緒

> d <- cbind(a,b,c)
> d[2,3]
[1] 10
> d[2,]
 a  b  c
 2  6 10
> d[,3]
[1]  9 10 11 12
> d[c(-2,-4),]
     a b  c
[1,] 1 5  9
[2,] 3 7 11

行列の基本演算

行列作って、足し算
直感的

> a <- matrix(c(1,2,3,4),2,2,byrow=T)
> b <- matrix(c(1,2,3,4),2,2,byrow=T)
> a+b
     [,1] [,2]
[1,]    2    4
[2,]    6    8

積がやっかい

「*」にしちゃうと積にならないよ

> a*b
     [,1] [,2]
[1,]    1    4
[2,]    9   16

積を求めたいときは「%*%」を使うべし

> a%*%b
     [,1] [,2]
[1,]    7   10
[2,]   15   22

逆行列を求める

solve関数

> solve(a)
     [,1] [,2]
[1,] -2.0  1.0
[2,]  1.5 -0.5

ちなみに

単位行列になりました
ゴミの範囲

> solve(a)%*%a
             [,1] [,2]
[1,] 1.000000e-00    0
[2,] 1.110223e-16    1

行列式

det関数

> det(a)
[1] -2

固有値

簡単

> eigen(a)
$values
[1]  5.3722813 -0.3722813

$vectors
           [,1]       [,2]
[1,] -0.4159736 -0.8245648
[2,] -0.9093767  0.5657675

配列

飛ばします

> summary(lm(speed~dist,data=cars))

Call:
lm(formula = speed ~ dist, data = cars)

Residuals:
    Min      1Q  Median      3Q     Max 
-7.5293 -2.1550  0.3615  2.4377  6.4179 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  8.28391    0.87438   9.474 1.44e-12 ***
dist         0.16557    0.01749   9.464 1.49e-12 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 

Residual standard error: 3.156 on 48 degrees of freedom
Multiple R-squared: 0.6511,	Adjusted R-squared: 0.6438 
F-statistic: 89.57 on 1 and 48 DF,  p-value: 1.490e-12

データフレーム

見た目はほとんど行列と同じ
行と列にラベルを持っていることが特徴
「$」でアクセスしたりするやつです
注意
- ベクトル構造は同じ長さ
- 行列構造は同じ行サイズ
どうしてもそれでダメなら
- 配列
- リスト
- とかを使ってください

例

とりあえずデータフレームにいれたいベクトルを用意

> ID1 <- c(1,2,3,4,5)
> VISIT1 <- c(10,20,30,10,50)
> SEX1 <- c("F","M","M","F","F")
> WEIGHT <- c(30,20,90,40,30)

データフレームを作る

data.frame関数

> A <- data.frame(id=ID1,vit=VISIT1,sex=SEX1,w=WEIGHT)
> A
  id vit sex  w
1  1  10   F 30
2  2  20   M 20
3  3  30   M 90
4  4  10   F 40
5  5  50   F 30

データフレームに列を追加と削除

「$」付けてベクトルを代入
列を削除したいときにはNULLを代入
cbindでもできる
mergeという関数もある

> A$test <- c(1,2,3,4,5)
> A
  id vit sex  w test
1  1  10   F 30    1
2  2  20   M 20    2
3  3  30   M 90    3
4  4  10   F 40    4
5  5  50   F 30    5
> A$test<-NULL
> A
  id vit sex  w
1  1  10   F 30
2  2  20   M 20
3  3  30   M 90
4  4  10   F 40
5  5  50   F 30

データフレームに行を追加

rbind

> rbind(A,c(2,20,"M",60))
  id vit sex  w
1  1  10   F 30
2  2  20   M 20
3  3  30   M 90
4  4  10   F 40
5  5  50   F 30
6  2  20   M 60

因子型

しばらくこの前まで何のためにあるやつか分かっていなかった＞＜
でも、これを使えるようになると便利

irisのデータでやってみる

あやめのデータ
よく使われるデータ
よい性質を持っているから

irisデータ

それぞれ50個ずついるよ

> summary(iris$Species)
    setosa versicolor  virginica
        50         50         50

層別にSepal.Lengthの長さを調べてみる

> tapply(iris$Sepal.Length,iris$Species,mean)
    setosa versicolor  virginica 
     5.006      5.936      6.588

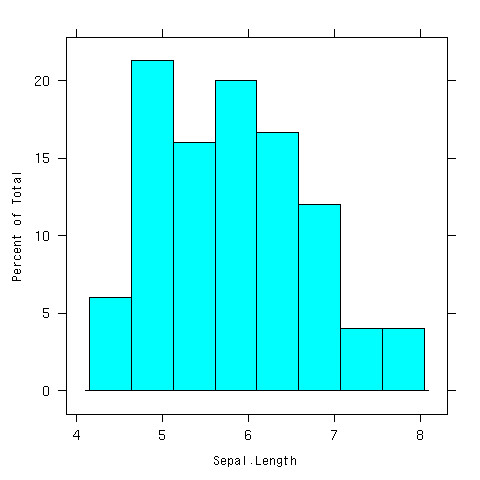
ヒストグラムを書いてみよう

> library(lattice)
> histogram(~Sepal.Length,data=iris)

できあがり

普通のヒストグラムと一緒じゃん
違うよ、全然違うよ

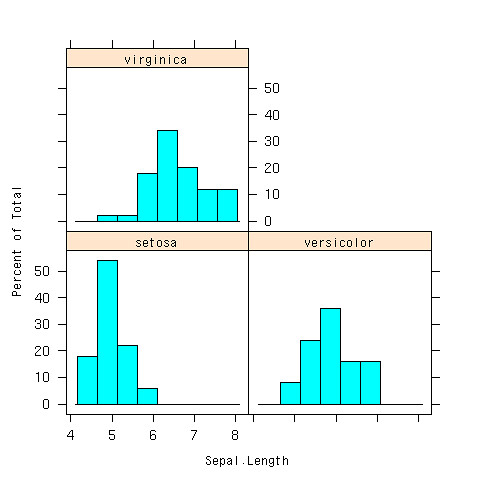
層別にヒスとグラムを書けるのがlatticeライブラリのhistgram

分布が違うね、とかいうことが分かる

> histogram(~Sepal.Length|Species,data=iris)

層別に統計量を出してくれるのがby関数

第一引数に求めたいデータ
第二引数に層別するもとのデータ
第三引数に求めたい統計量
- mean
- var

> by(iris$Sepal.Length,iris$Species,summary)
INDICES: setosa
   Min. 1st Qu.  Median    Mean 3rd Qu.    Max.
  4.300   4.800   5.000   5.006   5.200   5.800
------------------------------------------------------------
INDICES: versicolor
   Min. 1st Qu.  Median    Mean 3rd Qu.    Max.
  4.900   5.600   5.900   5.936   6.300   7.000
------------------------------------------------------------
INDICES: virginica
   Min. 1st Qu.  Median    Mean 3rd Qu.    Max.
  4.900   6.225   6.500   6.588   6.900   7.900

行列やデータフレームを持ってくることもできる

それぞれの列に対して層別された統計量を求める

> by(x[1:4],iris$Species,mean)
iris$Species: setosa
Sepal.Length  Sepal.Width Petal.Length  Petal.Width
       5.006        3.428        1.462        0.246
------------------------------------------------------------
iris$Species: versicolor
Sepal.Length  Sepal.Width Petal.Length  Petal.Width
       5.936        2.770        4.260        1.326
------------------------------------------------------------
iris$Species: virginica
Sepal.Length  Sepal.Width Petal.Length  Petal.Width
       6.588        2.974        5.552        2.026

層別で頻度を集計する

条件を付けたりすることができる

> xtabs(~Species,data=iris,Sepal.Width>3)
Species
    setosa versicolor  virginica
        42          8         17

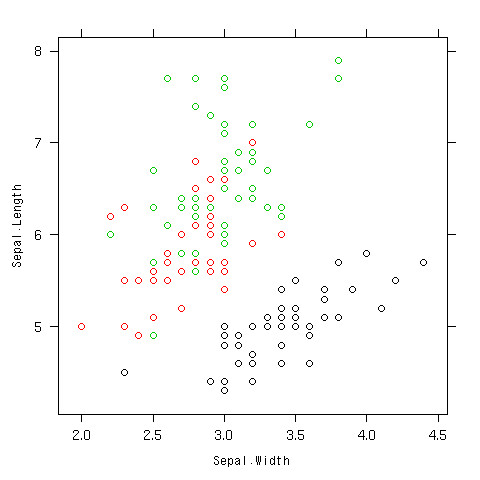
散布図を層別で書いてみる

色分け
他にもいろいろオプションはあるよ
ヘルプで見てね

> xyplot(Sepal.Length~Sepal.Width,data=iris,col=as.integer(iris$Species))

できあがり

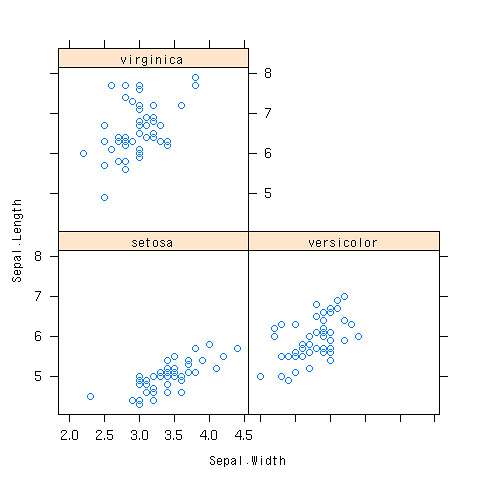
配布する資料が白黒だったら。。。

そもそも散布図を3つ書けばよい
「|」の後に因子データを持ってくる

> xyplot(Sepal.Length~Sepal.Width|Species,data=iris)

できあがり

irisのデータで相関係数行列を求めよう

5列目は因子だから要らない

> cor(iris[1:4])
             Sepal.Length Sepal.Width Petal.Length Petal.Width
Sepal.Length    1.0000000  -0.1175698    0.8717538   0.8179411
Sepal.Width    -0.1175698   1.0000000   -0.4284401  -0.3661259
Petal.Length    0.8717538  -0.4284401    1.0000000   0.9628654
Petal.Width     0.8179411  -0.3661259    0.9628654   1.0000000

別解

「[-5]」と書くと5列目を抜いた行列を返してくれるよ

> cor(iris[-5])
             Sepal.Length Sepal.Width Petal.Length Petal.Width
Sepal.Length    1.0000000  -0.1175698    0.8717538   0.8179411
Sepal.Width    -0.1175698   1.0000000   -0.4284401  -0.3661259
Petal.Length    0.8717538  -0.4284401    1.0000000   0.9628654
Petal.Width     0.8179411  -0.3661259    0.9628654   1.0000000

相関係数には注意が必要

因果関係は教えてくれない
線形関係しか教えてくれない
相関係数は異常値に弱い

線形じゃないけど、明らかに関係がある例

相関係数はほぼ0

> cor(r,r2)
[1] -0.05030245

f:id:syou6162:20161024223146p:plain

r <- runif(50,min=-10,max=10)
r2 <- r^2+rnorm(50,sd=7)
plot(r,r2)

plot(iris[-5])

f:id:syou6162:20161024223213p:plain

データ構造編

ここまで

関数編

データ解析の時によく使う関数
(データ解析だけに限らない)関数

データ解析の時によく使う関数

summary
plot
str
head

sumamry関数

「総称的関数」と呼ばれる類い
引数のオブジェクトの種類によって、よしなにやってくれる関数

例えばデータフレーム

> summary(cars)
     speed           dist       
 Min.   : 4.0   Min.   :  2.00  
 1st Qu.:12.0   1st Qu.: 26.00  
 Median :15.0   Median : 36.00  
 Mean   :15.4   Mean   : 42.98  
 3rd Qu.:19.0   3rd Qu.: 56.00  
 Max.   :25.0   Max.   :120.00

例えばリストに対して

> summary(list(c(T,F,T),1:10,list(c("a","b"))))
     Length Class  Mode   
[1,]  3     -none- logical
[2,] 10     -none- numeric
[3,]  1     -none- list

例えばlmオブジェクト(回帰分析の結果)に対して

> lm(speed~dist,data=cars)

Call:
lm(formula = speed ~ dist, data = cars)

Coefficients:
(Intercept)         dist  
     8.2839       0.1656  

> summary(lm(speed~dist,data=cars))

Call:
lm(formula = speed ~ dist, data = cars)

Residuals:
    Min      1Q  Median      3Q     Max 
-7.5293 -2.1550  0.3615  2.4377  6.4179 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  8.28391    0.87438   9.474 1.44e-12 ***
dist         0.16557    0.01749   9.464 1.49e-12 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 

Residual standard error: 3.156 on 48 degrees of freedom
Multiple R-squared: 0.6511,	Adjusted R-squared: 0.6438 
F-statistic: 89.57 on 1 and 48 DF,  p-value: 1.490e-12

裏ではsummary関数が頑張っている

> methods("summary")
 [1] summary.Date           summary.POSIXct        summary.POSIXlt       
 [4] summary.aov            summary.aovlist        summary.connection    
 [7] summary.data.frame     summary.default        summary.ecdf*         
[10] summary.factor         summary.glm            summary.infl          
[13] summary.lm             summary.loess*         summary.manova        
[16] summary.matrix         summary.mlm            summary.nls*          
[19] summary.packageStatus* summary.ppr*           summary.prcomp*       
[22] summary.princomp*      summary.stepfun        summary.stl*          
[25] summary.table          summary.tukeysmooth*  

   Non-visible functions are asterisked

plot関数

これも「総称的関数」

1変数のデータに対して

plot(rnorm(1:10),type="l")

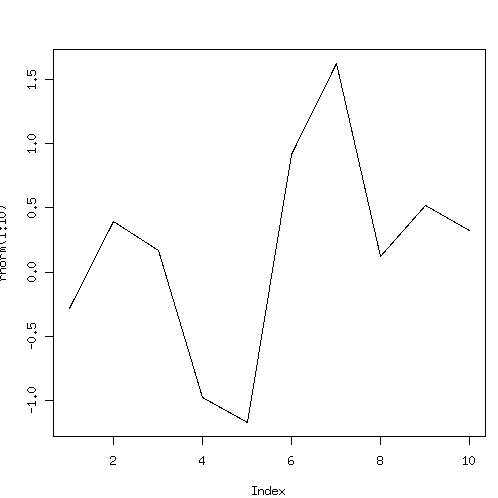
2変数のデータに対して

attach(cars)
plot(speed,dist)
detach(cars)
# with(cars,plot(speed,dist))

f:id:syou6162:20161024223301p:plain

時系列データに対して

plot(co2)

f:id:syou6162:20161024223328p:plain

裏ではplotが(ry

> methods("plot")
 [1] plot.Date*          plot.HoltWinters*   plot.POSIXct*      
 [4] plot.POSIXlt*       plot.TukeyHSD       plot.acf*          
 [7] plot.data.frame*    plot.decomposed.ts* plot.default       
[10] plot.dendrogram*    plot.density        plot.ecdf          
[13] plot.factor*        plot.formula*       plot.hclust*       
[16] plot.histogram*     plot.isoreg*        plot.lm            
[19] plot.medpolish*     plot.mlm            plot.ppr*          
[22] plot.prcomp*        plot.princomp*      plot.profile.nls*  
[25] plot.spec           plot.spec.coherency plot.spec.phase    
[28] plot.stepfun        plot.stl*           plot.table*        
[31] plot.ts             plot.tskernel*     

   Non-visible functions are asterisked

総称的関数のいいところ

マニアックな関数を知っていなくても、それとなくできてしまう
解析の時に、変なところに悩まなくてすむ

str関数

structure
データフレームやリストは慣れないと(慣れても)操作を間違いやすい

例えばリストの構造を見るとか

> str(list(c(T,F,T),1:10,list(c("a","b"))))
List of 3
 $ : logi [1:3]  TRUE FALSE  TRUE
 $ : int [1:10] 1 2 3 4 5 6 7 8 9 10
 $ :List of 1
  ..$ : chr [1:2] "a" "b"

例えばlmオブジェクトからp-valueのみを取り出したい時とか

> summary(lm(speed~dist,data=cars))

Call:
lm(formula = speed ~ dist, data = cars)

Residuals:
    Min      1Q  Median      3Q     Max 
-7.5293 -2.1550  0.3615  2.4377  6.4179 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  8.28391    0.87438   9.474 1.44e-12 ***
dist         0.16557    0.01749   9.464 1.49e-12 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 

Residual standard error: 3.156 on 48 degrees of freedom
Multiple R-squared: 0.6511,	Adjusted R-squared: 0.6438 
F-statistic: 89.57 on 1 and 48 DF,  p-value: 1.490e-12 
> summary(lm(speed~dist,data=cars))$coefficients[7]
[1] 1.440974e-12

やっていく過程

「リストからなってるんだなー」
「リストの$coefficientsがそれっぽいなー」
「最後のほうだから8番目とか?」

str(summary(lm(speed~dist,data=cars)))

head関数

これは軽め

> head(cars)
  speed dist
1     4    2
2     4   10
3     7    4
4     7   22
5     8   16
6     9   10

(データ解析だけに限らない)関数

関数定義

Rではもちろん自分で関数を定義することができる

hoge <- function(x){
  return(x^3)
}
> hoge(1:10)
 [1]    1    8   27   64  125  216  343  512  729 1000

ディフォルト値

割と便利
- Rubyみたいな感じで

例

explode <- function(x="skylab13"){
  cat(x,"爆発しろ!!",fill=TRUE)
}

> explode("misho")
misho 爆発しろ!!
> explode()
skylab13 爆発しろ!!

無名関数も、もちろんできる

> (function(x){for(i in seq(10)){cat(x,"かわいいよ",x,fill=TRUE)}})("λ")
λ かわいいよ λ
λ かわいいよ λ
λ かわいいよ λ
λ かわいいよ λ
λ かわいいよ λ
λ かわいいよ λ
λ かわいいよ λ
λ かわいいよ λ
λ かわいいよ λ
λ かわいいよ λ

Rにおける無名関数の使いどころは?

apply familyと呼ばれる関数群がある
引数に関数を取ることができる

> apply(cars,2,function(x){list(sum=sum(x),var=var(x))})
$speed
$speed$sum
[1] 770

$speed$var
[1] 27.95918


$dist
$dist$sum
[1] 2149

$dist$var
[1] 664.0608