トップ > R > R勉強会第三回

R勉強会第三回

R 勉強会

ここに資料を張る予定だよ＞＜。頑張って今日中に上げれるようにしとくよ＞＜。マーケティング工学の宿題全然終わってないよ＞＜。でも、とりあえずできてる分だけ置いとくよ＞＜。

R勉強会第三回

  • Presented by 吉田康久

前回は?

  • データ型
  • データ構造
    • データフレームなど
  • かなり飛ばした感じがあるので、また詳しくやるかと
  • 前回来てない人も大丈夫なように教えます

今回は?

  • 回帰分析
    • 重回帰分析
  • マーケティング工学
  • データ解析
  • みんなもっと楽にやろうよ!
  • みんなコマンドの意味とか、回帰分析に必要なこときちんとやろうよ!

今回の主役

  • lm
    • Fitting Linear Models
  • 単回帰も重回帰も
  • lmのテンプレート
> lm(formula, data, weights, subset, na.action)

説明

formula モデル式を明示する部分
data 任意のデータフレーム
weight 一俵でないウエイトを必要とする場合に、正の加重ベクトルを加えるための引数
subset 使用するデータの部分を明示するための添字ベクトル
na.action 欠損値の扱いを特定する関数

最初は…

  • lm(従属変数 ~ 説明変数1+説明変数2+…)
  • で覚えておいてもらって大丈夫
  • 係数は書かなくっていいよ

例

  • whiteside
  • 防寒壁を設置することでガス消費料への影響を調べる
Insul 防寒壁を設置する前を表すBeforeとAfterの因子
Temp 摂氏で計った週ごとの外気の平均気温
Gas 1000立方フィート単位で計った週ごとのガス消費料 
> library(MASS)

単回帰を当てはめる

  • 切片項は指定しなくても勝手に付いてくれる
  • 「-1」とかやると切片項を抜いてできるよ
> gasB<-lm(Gas~Temp,whiteside,subset=(Insul=="Before"))
> gasB

Call:
lm(formula = Gas ~ Temp, data = whiteside, subset = (Insul == "Before"))

Coefficients:
(Intercept)         Temp  
     6.8538      -0.3932

解説

  • call
    • 回帰モデルの式
  • Coefficients
    • それぞれに付く係数

もっと知りたい

  • 係数のt値とか
  • R^2とか
  • lm関数の結果にsummary関数を使おう

回帰モデルの精度

  • こんな風にやってね＞＜
> summary(gasB)
Call:
lm(formula = Gas ~ Temp, data = whiteside, subset = (Insul == 
    "Before"))

Residuals:
     Min       1Q   Median       3Q      Max 
-0.62020 -0.19947  0.06068  0.16770  0.59778 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  6.85383    0.11842   57.88   <2e-16 ******
Temp        -0.39324    0.01959  -20.08   <2e-16 ******
---
Signif. codes:  0 '******' 0.001 '****' 0.01 '**' 0.05 '.' 0.1 ' ' 1 

Residual standard error: 0.2813 on 24 degrees of freedom
Multiple R-Squared: 0.9438,	Adjusted R-squared: 0.9415 
F-statistic: 403.1 on 1 and 24 DF,  p-value: < 2.2e-16

意味を読み取る

  • Pr(>|t|)
    • 係数が有意なものか
    • 「.」くらいで採用。印が付いてないものはほぼ0となり、意味がない。
  • Multiple R-Squared
    • R^2のこと
  • Adjusted R-squared
    • 自由度修正済R^2のこと

意味を読み取る2

  • 重回帰では普通、自由度修正済R^2を見ていく
    • R^2は説明変数の数を増やすだけで上がってしまうから
  • F-statistic
    • F統計量。R^2が有意なものか計るために指標
  • 詳しいことは統計勉強会のほうでどうぞ＞＜

formulaについて

  • formulaって何?
    • 回帰モデルに使う式のこと
    • 「~」がついてたやつのこと
  • formulaを使いこなすと複雑になりがちな回帰式も簡単に書くことができる
  • lmには変数代入だけで済む
    • 変数変換
    • 交互作用

簡単な例

  • マーケティング工学で使うデータでやってみた
  • まあ、これくらいじゃわざわざformulaを使うまでもない
> formula<-price~x1+x2+x3
> formula
price ~ x1 + x2 + x3
> lm(formula)

Call:
lm(formula = formula)

Coefficients:
(Intercept)           x1           x2           x3
   125.4121      -6.3239       1.5256       0.3859

交互作用も入れた例

  • 交互作用は説明しなくてもいいですよね
  • 3変数で交互作用を書こうとすると結構大変
  • 切片項も含めると8個も書かないといけない
    • 切片項は書かなくても勝手に含まれるけど
    • いれたくなかったら0か-1を明示的に書く必要がある
    • 組合せ的に爆発してしまうので、formulaをうまく活用しよう

交互作用を簡単に書けるformula

> formula<-price~x1**x2**x3
> formula
price ~ x1 ** x2 ** x3
> lm(formula)

Call:
lm(formula = formula)

Coefficients:
(Intercept)           x1           x2           x3        x1:x2        x1:x3
   125.9396      -6.8293       0.5453      -0.1585       0.7148       0.6554
      x2:x3     x1:x2:x3
     2.7716      -1.6989

ちょっと外れて…

  • 交互作用とか考えずにx1**x2**x3の項とかで回帰モデルを作りたいよ
    • そういうときがあるかよく分かりませんが…
  • formulaの知識としてあるのは悪くないと思います
  • 「:」とか「I()」を使うと交互作用の項だけを書くことができる

コード

  • ごちゃごちゃになりやすいので注意
> formula<-price~x1:x2:x3
> lm(formula)

Call:
lm(formula = formula)

Coefficients:
(Intercept)     x1:x2:x3  
   119.6763      -0.7711  

> formula<-price~I(x1**x2**x3)
> lm(formula)

Call:
lm(formula = formula)

Coefficients:
    (Intercept)  I(x1 ** x2 ** x3)  
       119.6763          -0.7711

updateの仕方

  • モデルに変数の追加、削除の操作を行いたい
  • いちいち書き直してもいいけど…
  • 「今のモデルに…を付け加える」という操作のほうが直感的
  • それを行うのがupdate関数

update関数の例

  • まず、一説明変数からやってみる
  • よく見るやつ
> result1 <- lm(log(Volume) ~ log(Girth), data = trees)
> summary(result1)
Call:
lm(formula = log(Volume) ~ log(Girth), data = trees)

Residuals:
      Min        1Q    Median        3Q       Max 
-0.205999 -0.068702  0.001011  0.072585  0.247963 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) -2.35332    0.23066  -10.20 4.18e-11 ******
log(Girth)   2.19997    0.08983   24.49  < 2e-16 ******
---
Signif. codes:  0 '******' 0.001 '****' 0.01 '**' 0.05 '.' 0.1 ' ' 1 

Residual standard error: 0.115 on 29 degrees of freedom
Multiple R-Squared: 0.9539,	Adjusted R-squared: 0.9523 
F-statistic: 599.7 on 1 and 29 DF,  p-value: < 2.2e-16

update関数を使って説明変数の追加

  • 「.」は今モデルに入っている説明変数は全部使うよという意味
  • 「+」はその説明変数をモデルに使いしてね、という意味
> result2 <- update(result1, ~ . + log(Height), data = trees)
> summary(result2)
Call:
lm(formula = log(Volume) ~ log(Girth) + log(Height), data = trees)

Residuals:
      Min        1Q    Median        3Q       Max 
-0.168561 -0.048488  0.002431  0.063637  0.129223 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) -6.63162    0.79979  -8.292 5.06e-09 ******
log(Girth)   1.98265    0.07501  26.432  < 2e-16 ******
log(Height)  1.11712    0.20444   5.464 7.81e-06 ******
---
Signif. codes:  0 '******' 0.001 '****' 0.01 '**' 0.05 '.' 0.1 ' ' 1 

Residual standard error: 0.08139 on 28 degrees of freedom
Multiple R-Squared: 0.9777,	Adjusted R-squared: 0.9761 
F-statistic: 613.2 on 2 and 28 DF,  p-value: < 2.2e-16

update関数で説明変数を追加していけるけど…

  • なんでもかんでも説明変数に追加していい、というわけではない
  • 説明変数として追加してよいものかをみたい
    • 調整済み散布図

調整済み散布図

  • データ解析をやった人は知ってるやつです
  • 簡単に言うならば
    • 新しい変数を新たに加えることがどうか調べるためのもの
  • なぜそんなことを確かめる必要性があるのか
    • 多重共線性のため
    • 説明変数間に相関関係がある場合、相関係数行列を見るだけでは、重回帰モデルを視覚的に決定していくことができない
    • 調整済み散布図を書く必要がある
  • より詳しいことはデータ解析の講義を聞くとかしてください

調整済み散布図の書き方

  • まず、モデルに一つ説明変数が入っているモデルを考える
  • 横軸に新しくモデルに加えたい説明変数を既に入っている説明変数で回帰したモデルの残差
  • 縦軸にすでに組み込まれている説明変数を使って従属変数を回帰→その残差を取る

例

  • 従属変数はlog(Volume)、すでに組み込まれている説明変数はlog(Girth)
  • log(Height)を新たにモデルに加えたい
> x<-summary(lm(log(Height) ~ log(Girth), data = trees))$residuals
> y<-summary(lm(log(Volume) ~ log(Girth), data = trees))$residuals
> plot(x,y)

できあがり

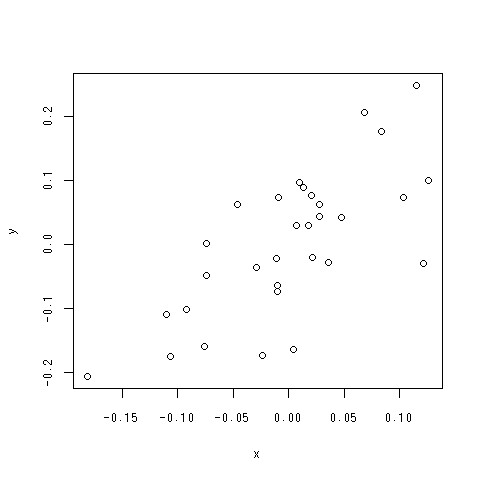
何を見ればよい?

  • 外れ値がないか
  • 全体として直線的な関係を保っていると言えるか
  • この場合は入れてよさそうですね
  • 理論モデルをやるならともかく、探索的データ解析などをやるときには多重共線性の問題が付きまとうので必ずやるようにしましょう
    • 「R^2が大きくなるから」とか言ってモデルに説明変数を加えるようなことがあると( ゜д゜)ゴラァ!と怒られます
    • 説明変数の選択自体は統計の本などにも載っていて、学類では習っていないテーマなので、興味ある人はyoshid50と一緒に勉強しましょう

予測値を知る

  • summary.lm関数を使って、係数情報を得て、説明変数のデータを投げて…というやり方でもできる
  • でも、面倒すぎる…
  • それpredict関数でできるよ

predict関数の使いかた

  • めちゃくちゃ簡単
  • 引数にlmオブジェクトを投げるだけ
  • あとで使うので、覚えといてね
> predict(result1)
       1        2        3        4        5        6        7        8 
2.302374 2.380487 2.431063 2.819630 2.861140 2.881605 2.921973 2.921973 
       9       10       11       12       13       14       15       16 
2.941882 2.961613 2.981168 3.000551 3.000551 3.057697 3.113395 3.272498 
      17       18       19       20       21       22       23       24 
3.272498 3.339678 3.404867 3.420867 3.452522 3.483728 3.529722 3.746287 
      25       26       27       28       29       30       31 
3.787154 3.918144 3.943431 3.993150 4.005406 4.005406 4.302224

モデルの選択

  • いろいろな方法がある
    • R^2
    • Cp基準
    • AIC
    • 尤度

R^2の問題点

  • とりあえず説明変数を増やせば、単調非減少
  • 欠点を補うべく修正済R^2が出てきた
    • しかし、R^2もまだまだ
    • 外れ値の影響を強く受ける
    • 経験的にモデルを過剰評価することが知られている(らしい)
  • 他にもモデルのよさを計る尺度が必要
    • Cp基準
      • データ解析でやったやつ
    • AIC
      • 赤池情報量基準
      • よく使われているようです
    • ベイズ統計量
      • 僕はよく知りません＞＜

Cp基準

  • 授業では説明変数の数とか残差をちょこちょこ計算していた
  • wleライブラリのmle.cp関数を使うと一発でできるよ
    • が、僕の環境でなぜか実行できなかったので、誰か代わりに試してみてください＞＜

AIC

  • AICは、「モデルの複雑さと、データとの適合度とのバランスを取る」ために使用される
    • by wikipedia
  • 説明変数を増やせば、データへのフィッティングもよくなるが、ノイズやそのデータ固有の情報に無理矢理あわせてしまうOverfittingの問題がある
  • そこでモデルの複雑度(説明変数の数など)とフィッティングのバランスを取る必要性がある
  • AIC=-2In(L)+2k(n/(n-k-1))
    • これ一冊で本が出ているので詳しくは紹介しません
  • AICの値が小さくなるほどよい

使いかた

  • 簡単です＞＜
> result1

Call:
lm(formula = log(Volume) ~ log(Girth), data = trees)

Coefficients:
(Intercept)   log(Girth)  
     -2.353        2.200  

> AIC(result1)
[1] -42.21102
  • 言いたいことは
  • 「R^2だけでモデル選択をすると危険なので、他にもモデル選択の基準があるんだよ」ってことを頭の隅においといてねってこと

誤差項の仮定

  • 独立性
  • 不偏性
  • 等分散性
  • 正規性
  • 誤差項は確率変数だよ
    • 難しかったら、今回は飛ばして聞いてもらっても構いません^^

でも、誤差項は

  • 真のパラメータが分かっているときのモデルとの差のこと
  • モデルのパラメータは推定値にしかすぎない
  • 回帰モデルが正しければ、残差は誤差に近似する
  • だから、残差を用いて前の仮定を診断していくよ!!

モデルの検定方法

  • 残差の正規性診断
  • 残差の分散の均一性

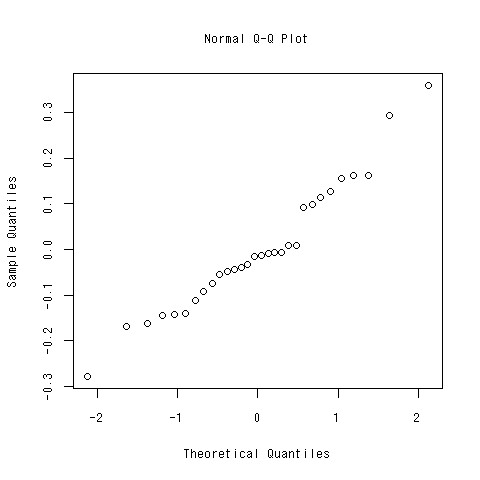
残差の正規性

  • 回帰分析をするときの仮定として、残差は正規分布に従うというものがあった
  • モデルの残差が正規分布に従っているか確かめないといけない
  • Rで確かめるには?
    • qqnormという関数

使いかた

  • qqnormに残差のベクトルを投げてやるだけ
  • これが直線に従っていれば残差は正規分布に従っていると言えるよ
    • 「もっと正確に何やってるか教えろ」って人は後で僕に聞いてください
> qqnorm(summary(lm(log(low.price)~.^2,data=car[,c(-1)]))$residuals)

できあがり

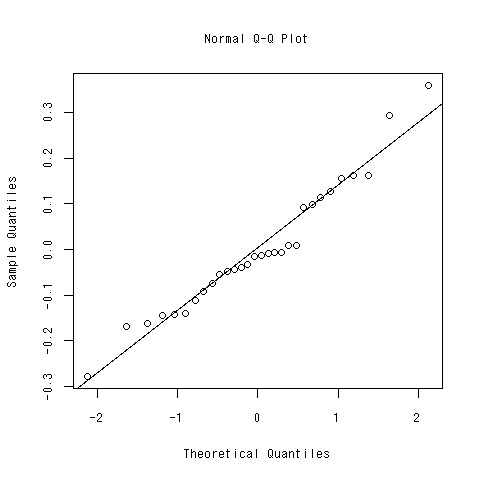
直線もついでに引こう

  • qqline関数
  • データ解析ではablineという関数を使って自分で直線を決めていた
> qqline(summary(lm(log(low.price)~.^2,data=car[,c(-1)]))$residuals)

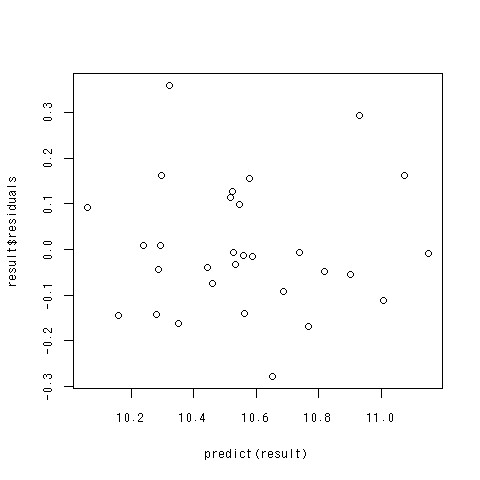
残差プロット

  • 回帰分析の仮定の続き
  • 残差の分散の均一性
    • 簡単に言うと「予測値が大きくなればなるほど、残差が大きくなる」とかそういう状況がおこっちゃだめだよ、ということ
  • 横軸に価格の予測値、縦軸に残差を取る
  • Rだと簡単にできるよ

残差プロットのコード

  • 実質、一行
> result<-lm(log(low.price)~.^2,data=car[,c(-1)])
> plot(predict(result),result$residuals)

できあがり

  • 予測値が大きくなるほど残差が大きくなるとかいう傾向が見られないので大丈夫そう。
    • 説明変数をとりあえず適当に選んだから、それでダメなんだけど。。。
    • 残差プロットの例ということでご勘弁。

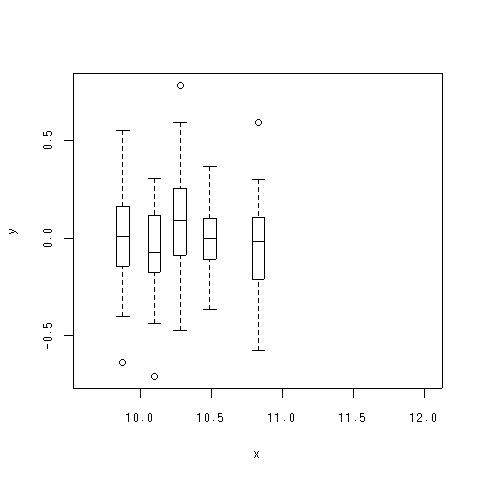
ちなみにデータ解析では

  • こんな感じのボックスプロットを並べて、分散の均一性を調べました
  • 見た目は違うけど、やってること一緒

さらにRでは

  • この2つを一回でやることができます

やり方

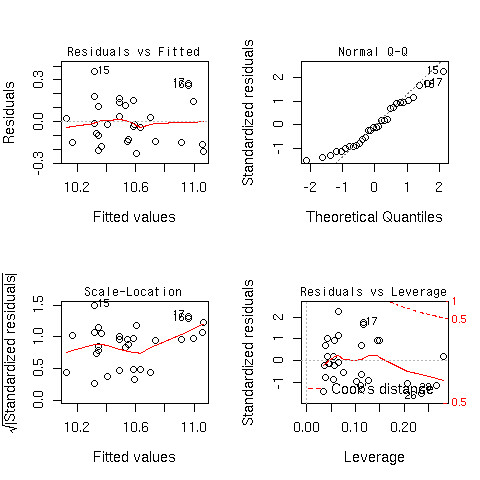
コード

> plot(lm(formula,data=car))

できあがり

おわり

…じゃなくて

  • 最初のふたつが分かっていれば、大丈夫
  • 一つ目のプロット
    • 残差プロット
  • 二つ目のプロット
    • 残差の正規性

さっき説明はしました

データフレームから欠損値を消す

  • 欠損値があるとうまく解析ができません
    • lmとかはやってくれるけど、あとでプロットとかができなくって困る
    • 対応する点がなくなっちゃうから
    • lmでは欠損値を無視している
  • is.na関数
  • データ解析では
> car[!is.na(car[1] & !is.na(car[2]))

大変

  • 欠損値を含む列がたくさんあるとis.naたくさんしないといけない
  • 面倒
  • やってられない

ためしにこういうデータ

> x <- c(1,3,2,1,NA,4)
> y <- c(2,NA,3,2,5,4)
> z <- c(5,3,2,3,2,1)
> w <- cbind(x,y,z)
> w
      x  y z
[1,]  1  2 5
[2,]  3 NA 3
[3,]  2  3 2
[4,]  1  2 3
[5,] NA  5 2
[6,]  4  4 1

NAがあるやつを全部抜く

  • complete.cases関数
  • 論理値のandを取る
> complete.cases(w)
[1]  TRUE FALSE  TRUE  TRUE FALSE  TRUE

> w[complete.cases(w),]

complete.casesを使う際の注意点

  • complete.cases関数便利
  • 欠損値はどんどん削っちゃえ
  • ちょっと待った
    • それはいけない
    • 欠損値だからと言って簡単に解析から省くようなことはしてはいけない
    • 調べるなりして埋める努力を
    • 欠損値として省くためには省くなりの理由を
  • データ解析を受けてね

今回扱わなかったテーマ

  • lsfitを使った回帰分析
  • anovaを使ったモデルの分散分析