データ解析のレポートを出すときには必ず見直すこと。
重回帰において、説明変数を複数使う場合、説明変数に強い相関がある場合は、応答変数と説明変数の単純散布図から回帰の係数情報を読み取ることはできない!!
なぜならば、反例があるからである。以下のような例を考えてみよう。
x1<-c(0,1,2) x2<-c(1,-2,-3) y<-c(1,-1,-1)
この例はy=x1+x2となっている。
そして、以下のようなコマンドを使って、散布図行列を書く。
par(mfrow=c(2,2)) plot(x1,x2,xlim=c(-0.5,2.5),ylim=c(-4,2),xlab="first explanatory variable",ylab="second explanatory variable") par(new=F) plot(x1,x2,type="n",axes=F,xlab="",ylab="") plot(x1,y,xlim=c(-0.5,2.5),ylim=c(-1.5,1.5),xlab="first explanatory variable",ylab="response") plot(x2,y,xlim=c(-4,2),ylim=c(-1.5,1.5),xlab="second explanatory variable",ylab="response")
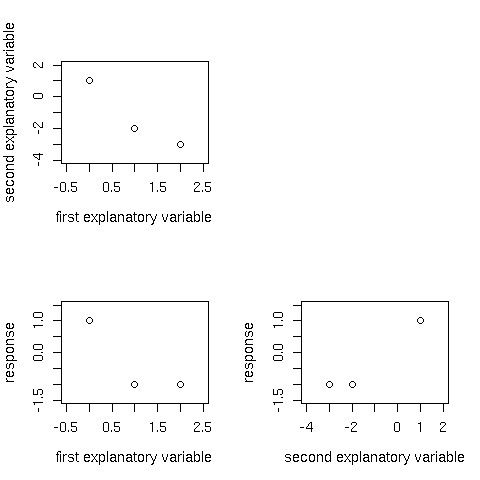
この図をよく見ると、説明変数x1とyの間に負の相関がある。これは係数が+1という情報と矛盾している。このことから、散布図行列を見て、「応答変数を説明するものとして使っていいな」と思ってはいけない例となっている。散布図行列はこのように説明変数間に強い相関が見られないかをチェックするためのものである。くれぐれも、この図から応答変数との相関を見て、判断するようなことがあってはならない。