この前の応用確率過程の課題をかっこよく見せる

内輪向け。普通、期待値の定義は
$E[X] = \int^{\infty}_{0}x f(x)dx$
で計算できるけど、分布関数が分かっているときは、分布関数を微分するまでもなく、以下の式で計算することができる。
$E[X] = \int^{\infty}_{0}[1-F(x)]dx$
で、この前の応用確率過程の中間試験のやり直しで、F(x)を適当に決めて、積分される範囲を示せっていう問題があった。俺はtexでレポート書いていたので、どうしようかと考えていたんだけど、Rでやることにした。指数分布でやってます。

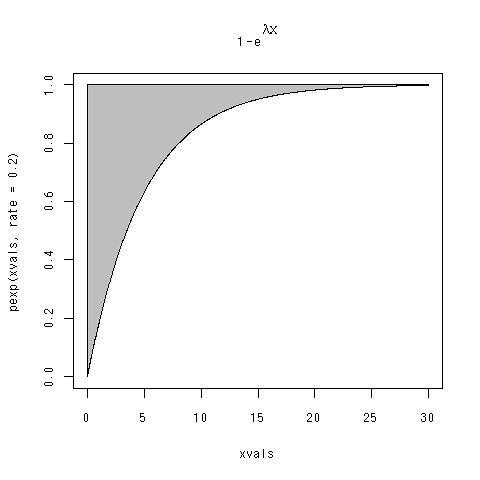
コードはこんな感じ。

xvals <- seq(0,30,length=1000)
plot(xvals,pexp(xvals,rate=0.2),type="l")
pvals <- pexp(xvals,rate=0.2)
polygon(c(xvals,rev(xvals)),c(rep(1,1000),rev(pvals)),col="grey")
title(main=expression(paste(1-plain(e)^{lambda * x})))