SIR(重点サンプリング)を簡単な例で

木曜だと思っていたゼミが明日だということにさっき気がついてあたふたと準備をしています。。。

担当している箇所はパターン認識と機械学習下 - ベイズ理論による統計的予測の11.1.4の重点サンプリングと11.1.5のSIRです。重点サンプリングのところは去年研究室の先輩と勉強会をやっていたときのちょっとしたコードが書き残していました。

Example of importance sampling - yasuhisa's blog

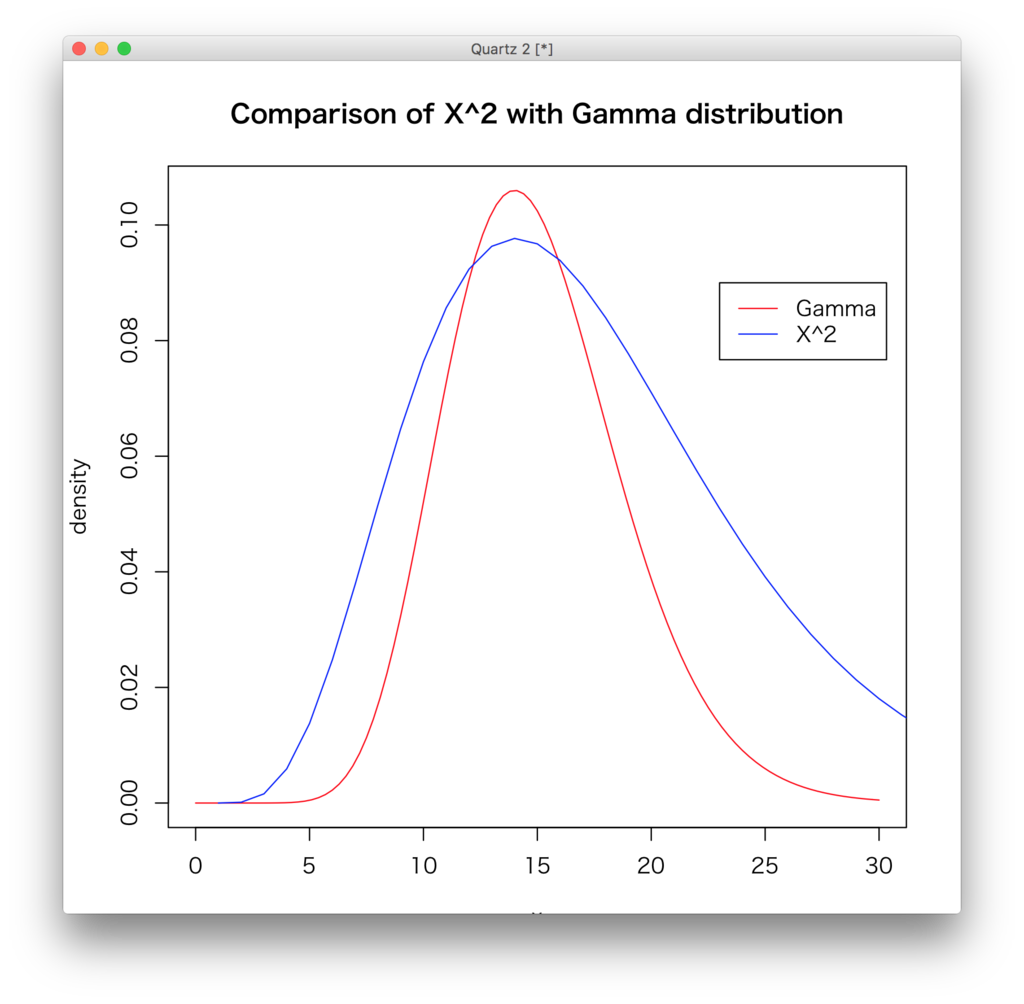
今年はガンマ分布のサンプリングから $X^2$ 分布のモーメントを推定するというのをやってみます。 $X^2$ 分布の一次モーメント(=平均)は自由度と一致します。ということでここでは、自由度を10としてみます(特に意味はない)。ガンマ分布のパラメータを適当に決めてあげて、密度関数をそれぞれplotしてみると以下のようになる。あんまり似てないかもだけど、まあいいじゃないですか。
f:id:syou6162:20161010130345p:plain
書くためのコード。

k <- 10 # X^2分布の自由度

# gamma分布のパラメータ
shape <- 15
rate <- 1

plot(function(x){dgamma(x, shape, rate)}, 0, 30, ylab="density", col="red")
title(main="Comparison of X^2 with Gamma distribution")
lines((function(x){dchisq(x, k)})(seq(0, 30, length.out=50)), col="blue")
legend(23, 0.09, c("Gamma", "X^2"), lwd=1, col=c("red", "blue"))

SIRのアルゴリズムは簡単である。3ステップしかない。計算統計学の方法―ブートストラップ・EMアルゴリズム・MCMC (シリーズ予測と発見の科学 5)のp161を参考にすると

g(x)を用いてM個の確率標本 $x_1, \cdots, x_M$ を発生させる
重み $w_j$ を $w_j \propto \pi(x_j) / g(x_j) , j = 1, \cdots, M$ とする
$(x_1, \cdots, x_M)$ の中から $m(\leq M)$ 個の確率標本xを復元抽出により確率 $Pr(x = x_j) = \frac{w_j }{\sum_{i=1}^M w_i}$ で発生させる

となっている。これだけである。ひょいひょいと実行できる(気をつけるのは、sampleのprobくらいか)。

> M <- 100000
> x <- rgamma(M, shape, rate)
> w <- dchisq(x, k) / dgamma(x, shape, rate)
> m <- 5000
> mean(sample(x, m, replace=TRUE, prob=w/sum(w))) # 復元抽出
[1] 10.05709

自由度が平均だったから、大体おkということである。M/m=20くらいがいいんじゃないかと計算統計学の方法―ブートストラップ・EMアルゴリズム・MCMC (シリーズ予測と発見の科学 5)に書いてあったので、それっぽいのを選んだ。

ちなみに、分布系も大体同じか見てみるとこんな感じになっており、欲しいものが取れていそうである。
f:id:syou6162:20161010130451p:plain
図のためのコード。

plot(function(x){dchisq(x, k)}, 0, 30, ylab="density")
lines(density(sample(x, m, replace=TRUE, prob=w/sum(w))), col="red")
legend(23, 0.09, c("X^2", "Estimated"), lwd=1, col=c("black", "red"))

簡単なので助かった。。。

追記

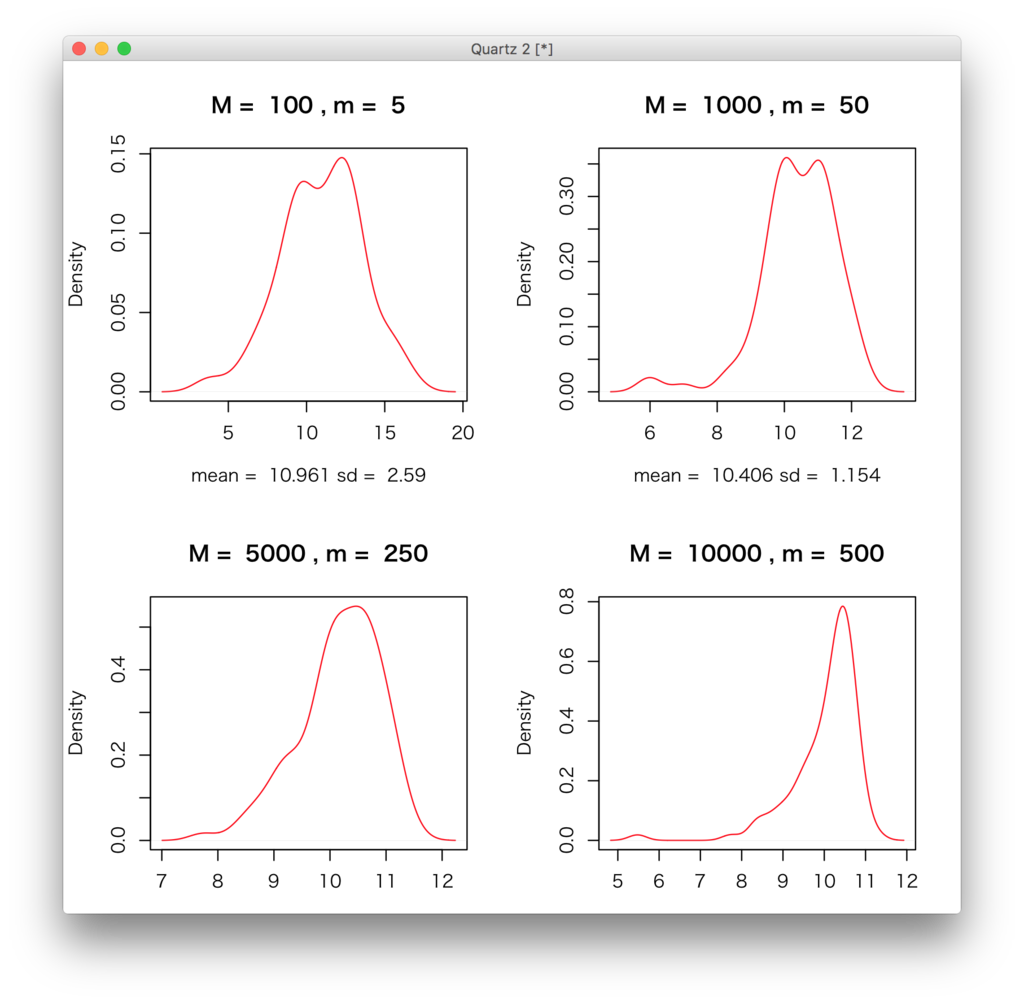
簡単とはいえ、Mとmでどれくらい平均の推定値がよくなるかについてちょっとくらいは実験しておかないと、、、という気になったので、実験した。M / m = 20の比は一定で、Mとmを変化させた。両方ともでかくしていくと真の値に一致していって、分散(標準誤差だけど)も小さくなっていくことが確認される。
f:id:syou6162:20161010130816p:plain
上のを書くためのコード。

make_estimator <- function(M, m) {
  x <- rgamma(M, shape, rate)
  w <- dchisq(x, k) / dgamma(x, shape, rate)
  mean(sample(x, m, replace=TRUE, prob=w/sum(w))) # 復元抽出
}

par(mfrow=c(2,2))

for(l in list(c(100, 5), c(1000, 50), c(5000, 250), c(10000, 500))) {
  M <- l[1]; m <- l[2]
  d <- sapply(1:100, function(x){make_estimator(M, m)})
  plot(density(d),
       main = paste("M = ", M, ", m = ", m),
       xlab = paste("mean = ", round(mean(d), 3), "sd = ", round(sd(d), 3)),
       ylab = "Density",
       col = "red")
}