Bootstrap法について色々書いてみる

2月に入ってから、Bootstrap Methods and their Application (Cambridge Series in Statistical and Probabilistic Mathematics)を読み始めている。で、数式はそこまでややこしくないのでわりと分かるんだが、Bootstrapを実行しなければならないシチュエーションというのが理解できていなかった。

nonparametricな場合はともかく、parametricな場合においてなんでこういうことが必要なケースがあるのかが理解できていなかった。「推定値の期待値とか推定値の分散って別にresamplingとかしなくても解析的に分かるからいいんじゃない?てか、頑張ってresamplingしたところで出てくるの一緒じゃね?」という感じである。

例があったほうがいいかもしれない。たぶん統計学の本ならどれにでも載っていそうな定理として次のようなものがある。

Let $X_1,\cdots,X_n$ be a random sample from a density $f(\cdot)$ , which has mean $\mu$ and finite variance $\sigma^2$ , and let $\bar{X}=(1/n)\sum^n_{i=1}X_i$ . Then $\mbox{E}[\bar{X}]=\mu$ and $\mbox{var}[\bar{X}]=\frac{1}{n}\sigma^2$ .

id:syou6162が普段使っているIntroduction to the Theory of StatisticsにもP231のTheorem 3で登場している。これはつまり、サンプル平均の期待値と分散がこういう感じで計算できるということを言っている。で、これはもうちょい強いことが言えて、サンプル平均は上で書いた平均と分散の正規分布に従う、ということも言える。これにより、( $\sigma^2$ を $S^2$ に置き替えたりして) $\mu$ の推定値 $\bar{X}$ の信頼区間などが分かり、おなじみの検定に持っていける、という感じである。ブートストラップのブの字も出てこなかった。

シミュレーション

bootstrapを使わない

Rを使ってシミュレーションをやってみよう。今回は指数分布を例にやってみる。指数分布の期待値は $1/\lambda$ 、分散は $1/\lambda^2$ と解析的に分かっている。ここではlambda=10、n=1000としてやってみることにしよう。解析的結果を用いると、

> lambda <- 10
> n <- 1000
> 1/lambda
[1] 0.1
> 1/(n*lambda^2)
[1] 1e-05

となり、サンプル平均の期待値と分散が計算できる。実際に指数分布に従う乱数を発生させてきて、真の分散を置きかえてやると

> x <- rexp(n,rate=lambda)
> mean(x)
[1] 0.1007655
> var(x)/n
[1] 1.080914e-05

極めて近い値になっているということが確認できる。サンプル平均の分布が正規分布に従うことも簡単に確認できる。

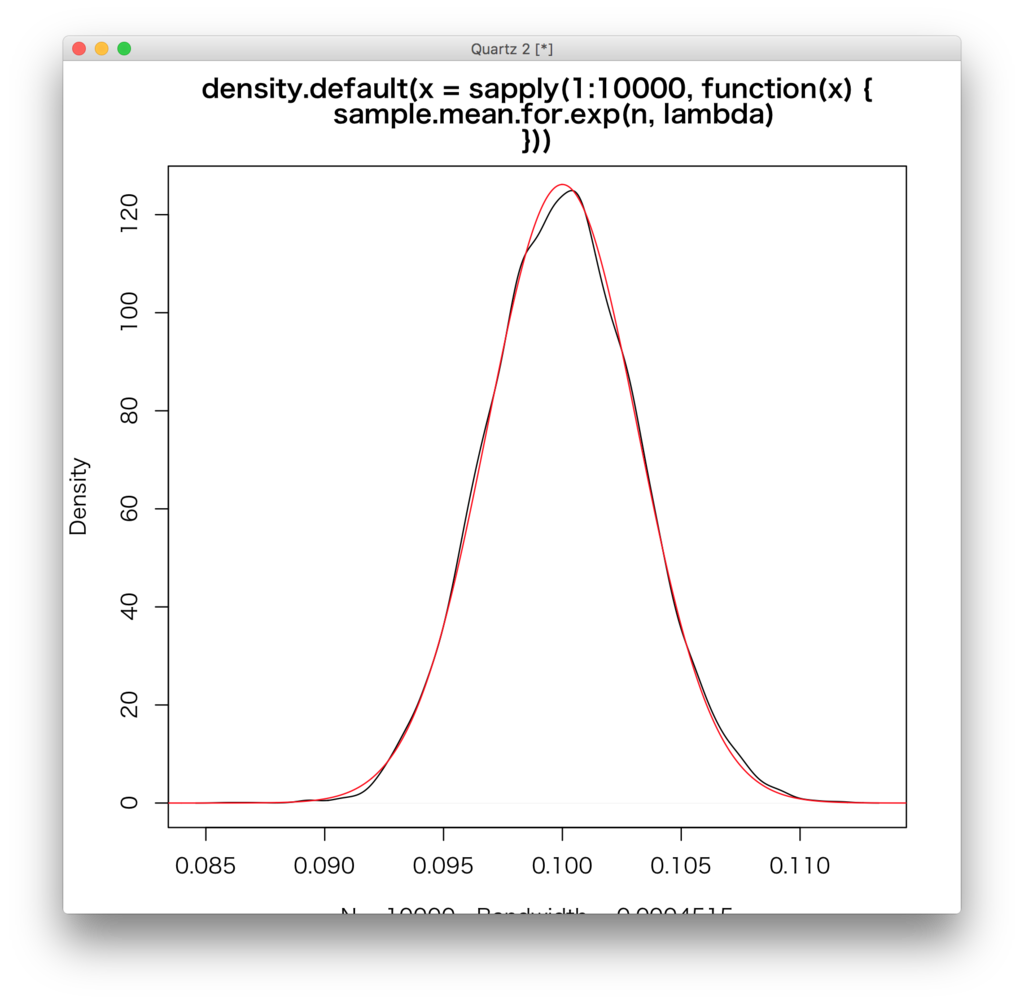
sample.mean.for.exp <- function(n,lambda){
  mean(rexp(n,rate=lambda))
}

plot(density(sapply(1:10000,function(x){sample.mean.for.exp(n,lambda)})))
s <- seq(0.08,0.12,length.out=1000)
lines(s,(function(x){dnorm(x,1/lambda,sqrt(1/(n*lambda^2)))})(s),col="red")

黒がサンプル平均の密度トレイス、赤が理論から計算される正規分布の密度関数となっている。
f:id:syou6162:20161103160710p:plain

bootstrapを使う

これをbootstrapな方法でやってみる。

lambda <- 10
n <- 1000
# 元データ
x <- rexp(n,rate=lambda)

# 平均の推定値
(esitimate <- mean(x))

R <- 999

# bootstrap sample
bs <- sapply(1:R,function(x){rexp(n,rate=esitimate)})

bootstrapによる推定値のよさの尺度にはbiasとvarianceがある。varianceについてはbootstrapでない方法のものとほぼ一致しているのが分かる。

> # bias
> 1 / R * sum(1 / apply(bs,2,mean)) - esitimate
[1] 9.796234e-05
> 
> # variance
> 1 / (R-1) * sum((
+                  1 / apply(bs,2,mean)
+                  -
+                  1 / R * sum(1 / apply(bs,2,mean))
+                  )^2)
[1] 1.069882e-05

密度トレイスをplotさせたもの。

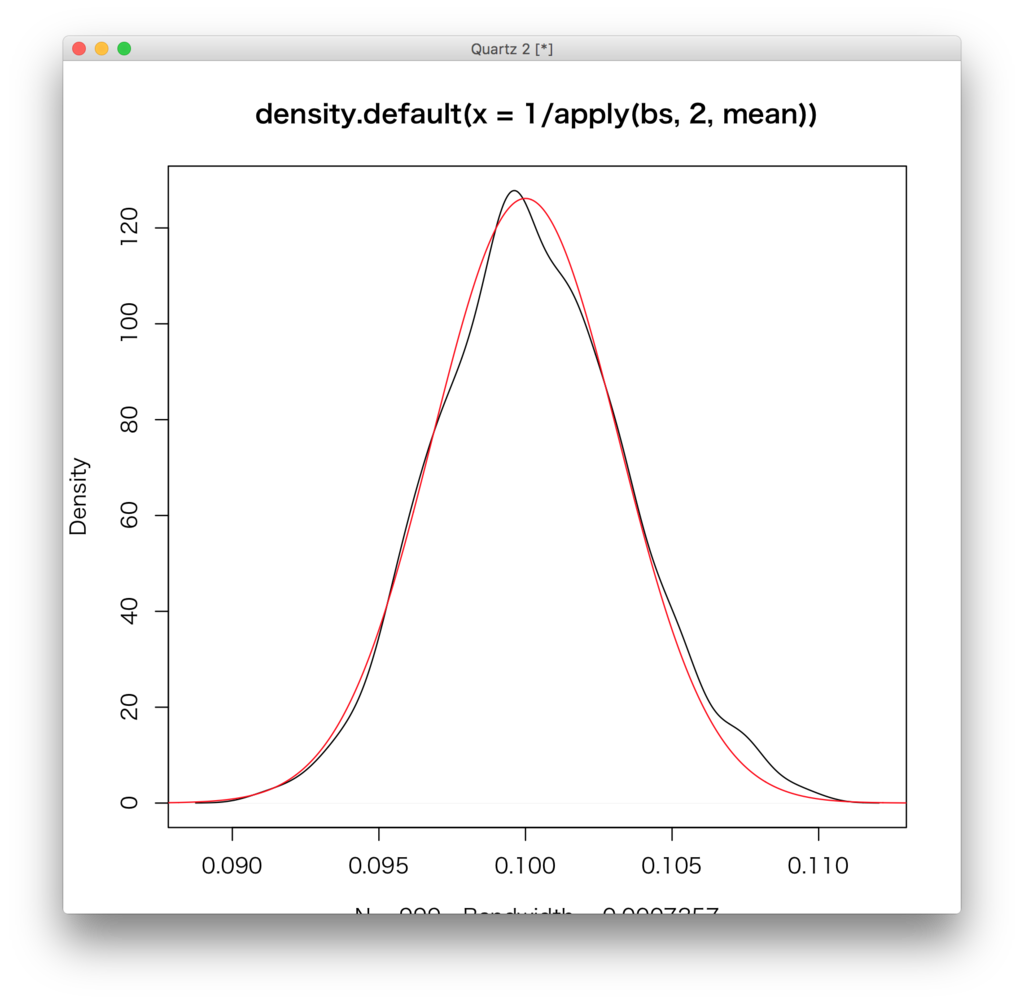
plot(density(1 / apply(bs,2,mean)))
s <- seq(0.08,0.12,length.out=1000)
lines(s,(function(x){dnorm(x,1/lambda,sqrt(1/(n*lambda^2)))})(s),col="red")

この場合は大体うまくいっていることが分かるが
f:id:syou6162:20161103160930p:plain
下のケースではうまくいっていないことが分かる。まあ、sampleによって違うのは当然と言えば当然。
f:id:syou6162:20161103160948p:plain
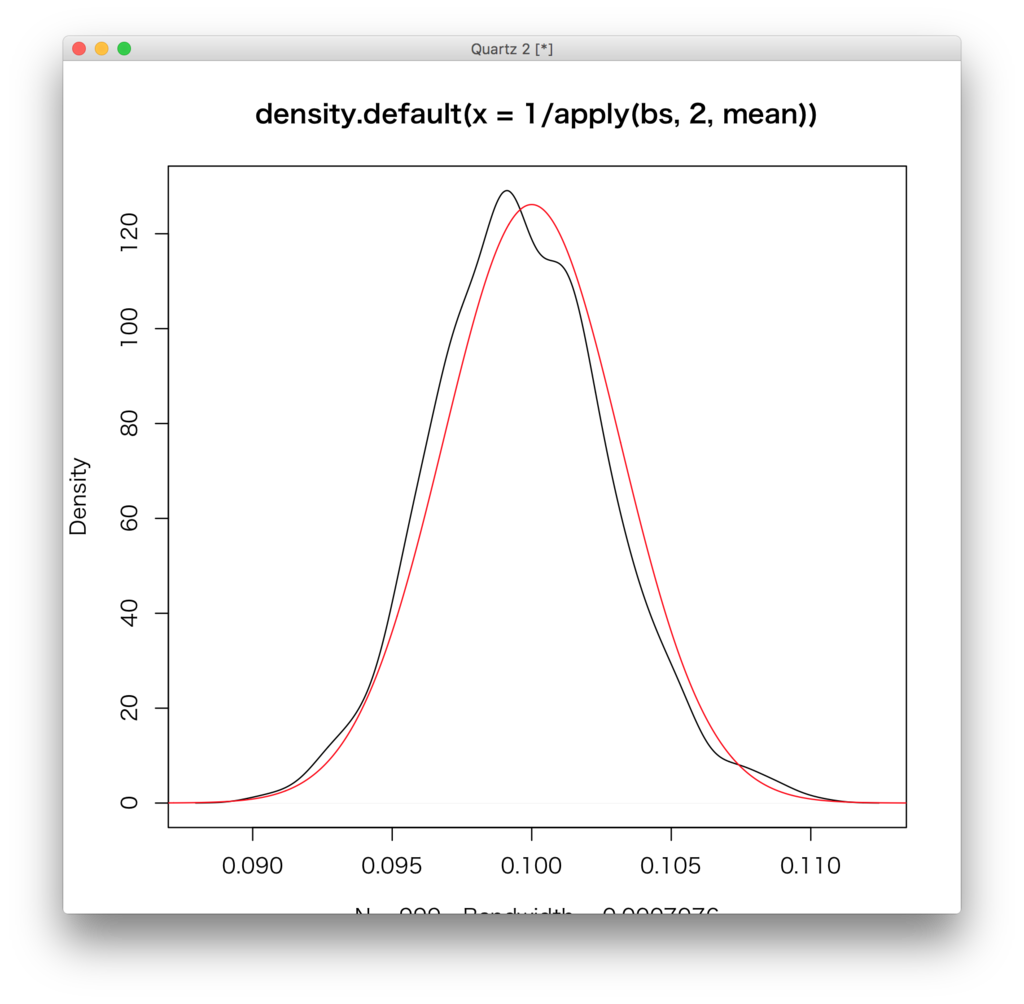
「sampleによって結構違うじゃん!!」と言われればそうなんだが、bootstrap法はよい性質を持っていて、 $n \rightarrow \infty$ の時いくつかの条件を課すとEDFが一致性を持つという性質がある。