多次元カーネル関数の色々なバージョンをplotしてみる

多変数におけるカーネル関数はいままでにいくつか扱ってきました。やったものとしては密度推定と、ナダラヤワトソン推定量による曲線回帰のようなものがあります。

これらにおけるカーネルには「乗法的である」という仮定を置いていました。カーネルが「乗法的である」というのは $K({\bf u}) = K(u_1) \times \cdots \times K(u_n)$ というようにカーネルの積の形で分解できるもののことを言います。また、直接プログラム中には出てきませんが、カーネル単回帰の時にもこの仮定は使っています*1。当たり前のように使いましたが、これらを仮定しない多次元カーネル関数というのももちろんあります。

多次元のカーネル関数の種類

多次元のカーネル関数の種類としては

乗法的カーネル関数であるという仮定を置いたもの
ユークリッドノルムを用いて定義してあるもの
バンド幅行列を用いて定義してあるより一般的なもの

の三種類に大別できます*2。

追記

種類というより、包含関係という感じか。

「乗法的カーネル関数の仮定を置いたもの」と「ユークリッドノルムで定義したもの」

ユークリッドノルムを用いて定義した2次元のEpanechnikovカーネル関数は、 $K({\bf u}) \propto (1 - {\bf u}^T {\bf u}) I({\bf u}^T {\bf u} \leq 1)$ となります。

ああ、言葉がいつもと違うから書いてて疲れてきた。元に戻そう。

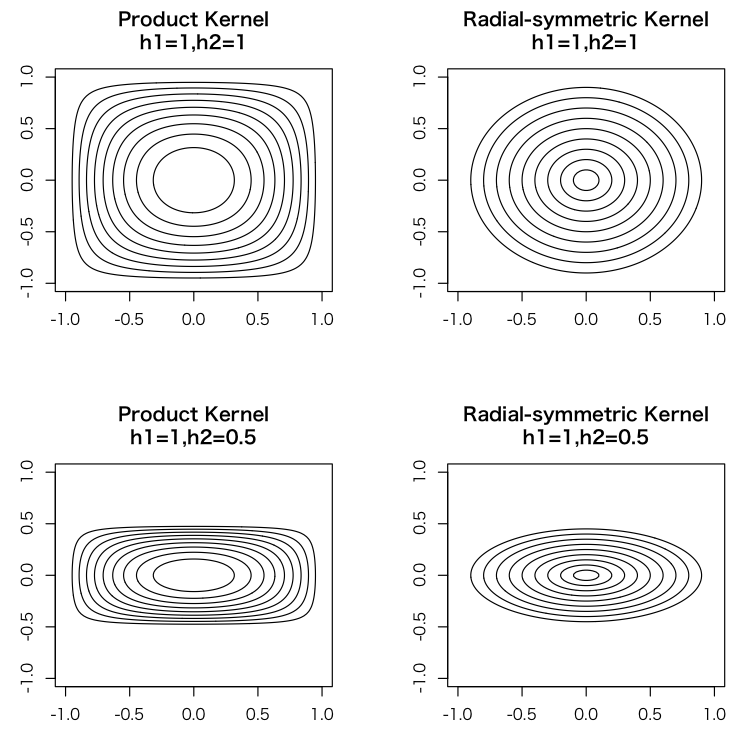
「乗法的カーネル関数の仮定を置いたもの」と「ユークリッドノルムで定義したもの」をバンド幅h1とh2を変更しつつplotしたのが下の画像。「乗法的カーネル関数の仮定を置いたもの」のほうは長方形みたいに、「ユークリッドノルムで定義したもの」は円なり楕円のような感じになる。

ソース

epanechnikov.product <- function(x1,x2,h1,h2){
  u1 <- x1/h1
  u2 <- x2/h2
  ((1-u1^2) * ifelse(abs(u1) <= 1,1,0)) *
    ((1-u2^2) * ifelse(abs(u2) <= 1,1,0))
}

epanechnikov.radial <- function(x1,x2,h1,h2){
  u1 <- x1/h1
  u2 <- x2/h2
  utu <- sqrt(u1*u1 + u2*u2)
  ((1-utu) * ifelse(utu <= 1,1,0))
}

s1 <- seq(-1,1,length.out=100)
s2 <- seq(-1,1,length.out=100)

par(mfrow=c(2,2))

mapply(function(h1,h2){
  contour.intern <- function(z,plot.title){
    contour(s1,s2,z,drawlabels=FALSE)
    title(main=paste(plot.title,"\nh1=",h1,",h2=",h2,sep=""))
  }
  z <- outer(s1,s2,function(x1,x2){epanechnikov.product(x1,x2,h1,h2)})
  contour.intern(z,"Product Kernel")
  z <- outer(s1,s2,function(x1,x2){epanechnikov.radial(x1,x2,h1,h2)})
  contour.intern(z,"Radial-symmetric Kernel")
}
       ,c(1,1),c(1,0.5))

バンド幅行列を用いて定義してあるより一般的なもの

バンド幅行列を用いた、より一般的な多変数カーネル関数の定義は次のようになっている。
$\hat{f_X}(x) = \frac{1}{n}\sum^n_{i=1}\frac{1}{|H|}K(H^{-1}(x-X_i))$

バンド幅行列を使ったやつというのは、要するに(バンド幅行列の逆行列を使って)基底を変換したようなものという感じのやつ。回転させたりとかそんなやつですね。

で、Nonparametric and Semiparametric Models (Springer Series in Statistics)のP69付近にこんな記述がある。

What effect has the inclusion of off-diagonal elements? We will see in Subsection 3.6.2 that a goog rule of thumb is to use a bandwidth matrix proportional to $\hat{\Sigma}^{-1/2}$ where $\hat{\Sigma}$ is the covariance matrix of the data. Hence, using such a bandwidth corresponds to a transformation of the data, so that they have an identity covariance matrix. As a consequence we can use bandwidth matrices to adjust for correlation between the components of X.

大体訳すると

非対角要素があるとどうなるのか?
データの分散共分散行列のマイナス1/2乗してやったやつをバンド幅行列に使ってやればいいっていうのが経験則から分かってるよ、っていうのが3.6.2に書いてあるよ
だから、そういうバンド幅は、データを変換することに対応するよ
結果として、Xの相関行列を使えばいいんじゃないかな!!

なんか文章がおかしいと思うんですけど、気にしない。。。3.6.2章を読めってことですね。。。

乗法的カーネル関数のやつはどう書けばいいのかなーと思ったけど、 $H^{-1}$ で変換してやってから、カーネルを分解してあげれば何も難しいことはないですね。

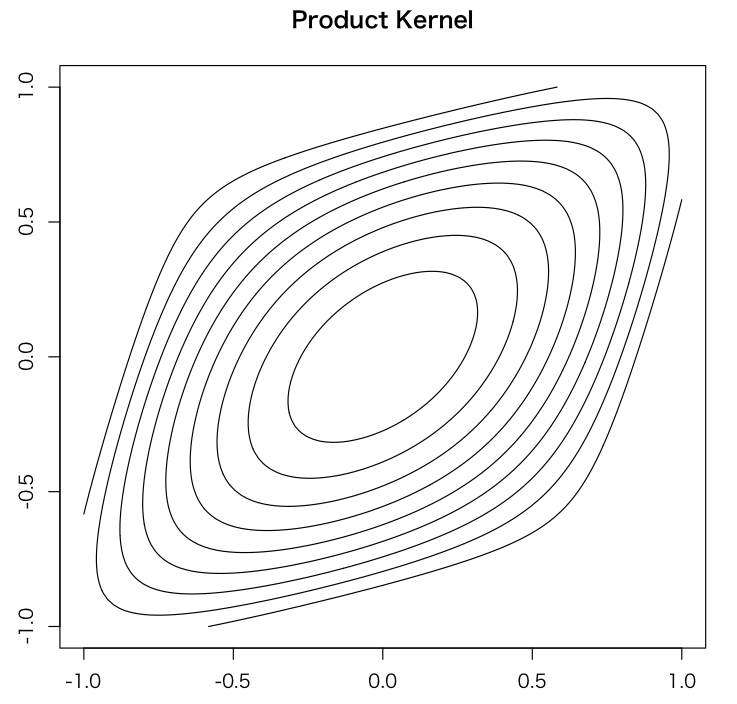
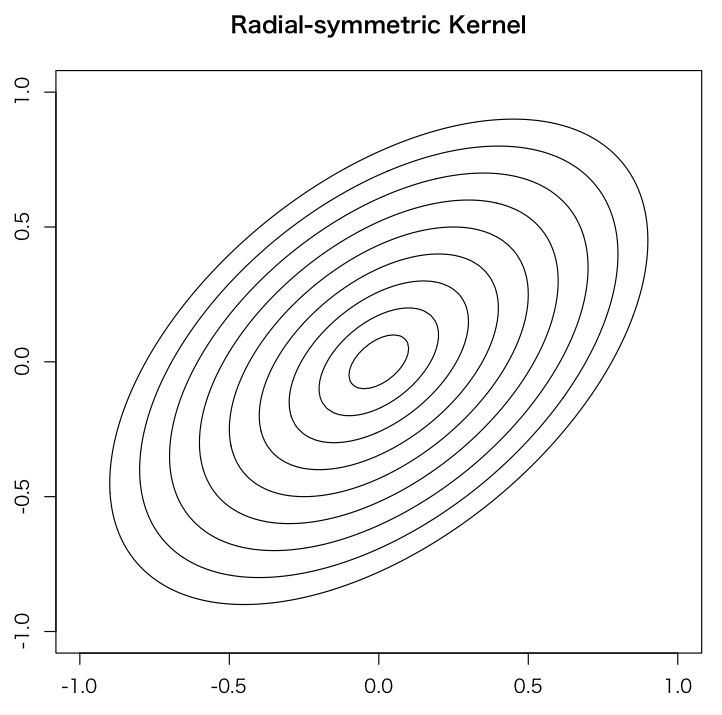
ソース

# http://cse.naro.affrc.go.jp/takezawa/r-tips/r/20.htmlを参考
A <- matrix(c(1,0.5,0.5,1),2,2)
U <- svd(A)$u
V <- svd(A)$v
D <- diag(sqrt(svd(A)$d))
H <- U %*% D %*% t(V)

epanechnikov.product <- function(x1,x2,H){
  inv.h <- solve(H)
  #outerを使うために、行列計算しないでやっている。。。
  u1 <- inv.h[1,1]*x1 + inv.h[1,2]*x2
  u2 <- inv.h[2,1]*x1 + inv.h[2,2]*x2
  ((1-u1^2) * ifelse(abs(u1) <= 1,1,0)) *
    ((1-u2^2) * ifelse(abs(u2) <= 1,1,0))
}

epanechnikov.radial <- function(x1,x2,H){
  inv.h <- solve(H)
  #outerを使うために、行列計算しないでやっている。。。
  u1 <- inv.h[1,1]*x1 + inv.h[1,2]*x2
  u2 <- inv.h[2,1]*x1 + inv.h[2,2]*x2
  utu <- sqrt(u1^2 + u2^2)
  ((1-utu) * ifelse(utu <= 1,1,0))
}

z <- outer(s1,s2,function(x1,x2){epanechnikov.product(x1,x2,H)})
contour(s1,s2,z,drawlabels=FALSE)
title("Product Kernel")

z <- outer(s1,s2,function(x1,x2){epanechnikov.radial(x1,x2,H)})
contour(s1,s2,z,drawlabels=FALSE)
title("Radial-symmetric Kernel")