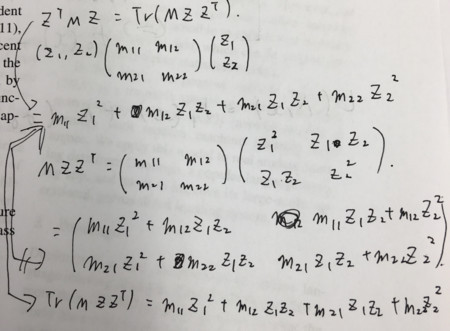社内で異常検知本の輪講を進めています。今回は近傍法による異常検知。一年くらいに一人で読んだときのメモはこちら。慣れない人は途中で出てくる劣モジュラの概念や勾配の導出が大変かなと思ったので、メモ書きしておきます。
劣勾配/劣勾配法
目的関数が連続で微分可能な関数の場合、SGDなどによって最適化が可能な場合がある。しかし、微分可能でない点を含む場合(機械学習の文脈ではヒンジ損失やL1正則化項など、様々なところで目にする)、単純な勾配法は使えない。しかし、勾配の概念を拡張した劣勾配法で最適化を行なえる場合がある。
連続で凸な関数fがあったときに、任意のに対して
を満たすようなを
におけるfの劣勾配という。勾配は一つの値であるが、劣勾配は条件を満たすものが複数存在することがあるので、値ではなく集合として与えられる。1次元で書くと分かりやすいが、右辺が傾きgで、点(a, f(a))を通る直線であり、左辺はそれより等しいか上にいるという条件を表わしている(fが微分可能で等号が成立している場合、いわゆる接線の方程式ってやつになってますね)。
図は劣勾配と劣微分の定義と意味 - 具体例で学ぶ数学より引用。f(x)よりも下にくるような直線は何本でも引けるため、劣勾配は集合というわけである。この劣勾配を使ってSGDのように最適化を行なうことを劣勾配法と呼ぶ。劣勾配を使って勾配法を行なった場合にも勾配法と似たような収束の議論ができる(参考リンク)。
目的関数の勾配
発表資料をWebに上げてくださっている方がすでにいらっしゃるので、そこを参考にしながら輪講を進めている。
42ページから勾配の導出の説明がされているが、本に書いてあるように行列のTraceの微分を使うともっとすっきりと書けるので、その方法についてメモしておく。というよく知られた関係を使う。これ自体は丁寧に書きくだすと簡単に導出できます。
とおいて、
が分かると勾配の式が大体出てくる。一般の式で示すのは若干面倒だけど、2x2くらいのサイズの行列で示してみると雰囲気が分かる。手書きが汚ないけど、こんな感じじゃ。元論文のAppendixを見るのもいいかもしれない。

- 作者: 井手剛,杉山将
- 出版社/メーカー: 講談社
- 発売日: 2015/08/08
- メディア: 単行本(ソフトカバー)
- この商品を含むブログ (2件) を見る