Rでニューラルネットワークをやってみる

ニューラルネットワークについて
プログラム
追記
nnetとかをもうちょっと
最適化とかヘッセ行列がらみの話

ニューラルネットワークについて

先週のPRMLでNNことニューラルネットワークについて勉強を始めました。PRMLは主に理論についての本なので、「ふーん」という感じなんですが、読書会後に「NNって(一定制約の元で)任意の関数に近似できることが証明されてるんだぜ?」とか言われると中二病患者の俺としては「?!NNってすごくね?てか、そんなすごいんだったらNNだけでいらなくね?他のモデルいらなくね?」とか思ってしまいます。しかし、直後に

あくまで近似。どれくらいの精度かはものによる
近似できないものも存在する*1

と教えてもらったので、他のモデルもちゃんと勉強する価値があるんだなと思い直したりしたんですが。なんとも浅はか...。

そんな感じで、自分で何かやってみるかと思い、Rでやってみることにしました。ちなみに単層パーセプトロンについてはライブラリとかを使わずに自分で昔書いたりしていました。

単層パーセプトロンだと統計屋さんから見たところのGLM(一般化線形モデル)と一緒やんという結論だったわけですが、今度は隠れ層とかも入れてやってみるわけです。今回も自分で実装してみてもいいんですが、ヘッセ行列とか入ってくるので、ライブラリでどんな感じになるのかを掴んでからでもいいかなーということでRのニューラルネットワークのパッケージnnetを使ってみることにしました。下の本を参考にしてやっています。9章の平滑化回帰のところ。

S‐PLUSによる統計解析

作者: W.N.ヴェナブルズ,B.D.リプリー,W.N. Venables,B.D. Ripley,伊藤幹夫,戸瀬信之,大津泰介,中東雅樹
出版社/メーカー: シュプリンガー・フェアラーク東京
発売日: 2001/07
メディア: 単行本
クリック: 9回
この商品を含むブログ (7件) を見る

Splusの本ですが、Rとコマンドがほぼ一緒です。こういうSplusのいい本も使えるというのがRの強いところですね!!、とRの宣伝をしたところで早速。

プログラム

データの準備

まず、ライブラリのロードとデータフレームの準備。

library(nnet)
attach(rock)

area1 <- area/10000; peri1 <- peri/10000
rock1 <- data.frame(perm, area=area1, peri=peri1, shape)

モデル式の作成

次にモデル式を作ります。「目的変数 ~ 説明変数」のようなformulaの付近は普通の回帰モデルと一緒だし*2、rock1の付近のデータの指定の付近もlmとかglmと一緒です。変に新しいことを覚えなくてもできてしまうR素敵!!

> rock.nn <- nnet(log(perm) ~ area + peri + shape, rock1,
+                 size=3, decay=1e-3, linout=T, skip=T, maxit=1000, Hess=T)
# weights:  19
initial  value 1749.939829 
iter  10 value 32.615819
iter  20 value 31.172037
iter  30 value 29.510679
iter  40 value 29.479555
iter  50 value 29.313074
iter  60 value 29.162789
iter  70 value 29.132618
iter  80 value 29.125367
iter  90 value 29.037367
iter 100 value 24.709824
iter 110 value 17.723236
iter 120 value 16.957107
iter 130 value 16.727941
iter 140 value 16.675815
iter 150 value 16.659896
iter 160 value 16.653732
iter 170 value 16.652433
iter 180 value 16.651559
iter 190 value 16.650859
iter 200 value 16.650288
iter 210 value 16.650118
iter 220 value 16.650037
iter 230 value 16.649983
iter 240 value 16.649946
final  value 16.649940 
converged

本に解説があるし、ヘルプを見れば分かるんだけど、引数の説明を少ししておくか。

引数	解説
size	隠れ層のユニット数
decay	lambdaの設定。正規化項の重み付けのようなやつですかね。PRMLでもよく登場しています。
maxit	iterationの最大回数の。止まらないことがないようにということでしょうか。上のはすぐ止まっているけど。
Hess	推定値に対するHesse行列を出力。

結果の表示

結果を見てみましょう。rock.nnとだけ書くとなんかそっけない感じですが、R userならsummaryやればどうにかなると知っているので、summary関数をやると詳しい結果を見ることができます。bはPRMLでいうところのバイアス項、iは入力層、hは隠れ層、oは最終的な出力層になっています。

> rock.nn
a 3-3-1 network with 19 weights
inputs: area peri shape 
output(s): log(perm) 
options were - skip-layer connections  linear output units  decay=0.001
> summary(rock.nn)
a 3-3-1 network with 19 weights
options were - skip-layer connections  linear output units  decay=0.001
 b->h1 i1->h1 i2->h1 i3->h1 
  2.83  -5.87  -6.89  -4.03 
 b->h2 i1->h2 i2->h2 i3->h2 
-11.56  11.94  12.66  -8.25 
 b->h3 i1->h3 i2->h3 i3->h3 
 -7.16  11.74 -11.87  -0.01 
  b->o  h1->o  h2->o  h3->o  i1->o  i2->o  i3->o 
 -4.21  12.27  -2.60  -9.09  24.62 -24.47   1.91

まあ、summaryでもいくつか出力を抑えているので、詳しいところとかもっと知りたかったらstr関数を使えばいいですね。これを元に煮るなり焼くなりすればいいと思います。

> str(rock.nn)
List of 19
 $ n            : num [1:3] 3 3 1
 $ nunits       : num 8
 $ nconn        : num [1:9] 0 0 0 0 0 4 8 12 19
 $ conn         : num [1:19] 0 1 2 3 0 1 2 3 0 1 ...
 $ nsunits      : num 7
 $ decay        : num 0.001
 $ entropy      : logi FALSE
 $ softmax      : logi FALSE
 $ censored     : logi FALSE
 $ value        : num 16.6
 $ wts          : num [1:19] 2.83 -5.87 -6.89 -4.03 -11.56 ...
 $ convergence  : int 0
 $ fitted.values: num [1:48, 1] 2.22 2.05 2.9 2.41 3.06 ...
  ..- attr(*, "dimnames")=List of 2
  .. ..$ : chr [1:48] "1" "2" "3" "4" ...
  .. ..$ : NULL
 $ residuals    : num [1:48, 1] -0.375 -0.204 -1.054 -0.568 -0.218 ...
  ..- attr(*, "dimnames")=List of 2
  .. ..$ : chr [1:48] "1" "2" "3" "4" ...
  .. ..$ : NULL
 $ call         : language nnet.formula(formula = log(perm) ~ area + peri + shape, data = rock1,      size = 3, decay = 0.001, linout = T, skip = T, maxit = 1000,  ...
 $ Hessian      : num [1:19, 1:19] 117.74 36.32 11.78 29.06 -2.47 ...
 $ terms        :Classes 'terms', 'formula' length 3 log(perm) ~ area + peri + shape
  .. ..- attr(*, "variables")= language list(log(perm), area, peri, shape)
  .. ..- attr(*, "factors")= int [1:4, 1:3] 0 1 0 0 0 0 1 0 0 0 ...
  .. .. ..- attr(*, "dimnames")=List of 2
  .. .. .. ..$ : chr [1:4] "log(perm)" "area" "peri" "shape"
  .. .. .. ..$ : chr [1:3] "area" "peri" "shape"
  .. ..- attr(*, "term.labels")= chr [1:3] "area" "peri" "shape"
  .. ..- attr(*, "order")= int [1:3] 1 1 1
  .. ..- attr(*, "intercept")= int 1
  .. ..- attr(*, "response")= int 1
  .. ..- attr(*, ".Environment")=<environment: R_GlobalEnv> 
  .. ..- attr(*, "predvars")= language list(log(perm), area, peri, shape)
  .. ..- attr(*, "dataClasses")= Named chr [1:4] "numeric" "numeric" "numeric" "numeric"
  .. .. ..- attr(*, "names")= chr [1:4] "log(perm)" "area" "peri" "shape"
 $ coefnames    : chr [1:3] "area" "peri" "shape"
 $ xlevels      : list()
 - attr(*, "class")= chr [1:2] "nnet.formula" "nnet"
>

予測値を得たい

予測値を得たい!!そんな時もRなので、変な関数を使う必要もなくてpredict関数があればよいです。二乗和誤差はこんな感じか。

> sum((log(perm) - predict(rock.nn))^2)
[1] 14.24258

rock1のattachはもう必要なさそうなので、適当にdetach。

> detach()

ヘッセ行列の固有値を見る

PRMLの240pに「これをD次元に拡張すると、 $w^*$ で評価されたヘッセ行列が正定値ならば $w^*$ は極小点である。」とあります。正定値ということはヘッセ行列の固有値が全て正である、ということです。そういうわけなので、ヘッセ行列の固有値を見てみましょう。固有値と言えばeigen。なお、固有行列はeigen(rock.nn$Hess, T)$vectorsでもできます。

> eigen(rock.nn$Hess, T)$values
 [1] 1.352569e+03 7.772788e+01 4.865793e+01 1.827773e+01 1.024351e+01
 [6] 4.091140e+00 1.215688e+00 8.518542e-01 5.326018e-01 3.540146e-01
[11] 1.366663e-01 7.656697e-02 2.846763e-02 1.341180e-02 1.012166e-02
[16] 7.031102e-03 6.028308e-03 4.009622e-03 3.265157e-03

おお、全部正になってるなあ。あれ、極小点であれば、ヘッセ行列は正定値っていうのは言えるんだっけ?とりあえず正定値なので、極小点であるということは言えますが。

ニューラルネットワークを可視化する

で、本のほうはこの辺で終わっているんですが、PRMLに載っているようなグラフ書きたいよね!ということでplot(rock.nn)やってみたんですが、動かない＞＜。これは予想外、なんですが北大の久保先生がNNをplotするための関数を作ってくださっています。おお、すげー。

source("http://hosho.ees.hokudai.ac.jp/~kubo/log/2007/img07/plot.nn.txt")
plot.nn(rock.nn)

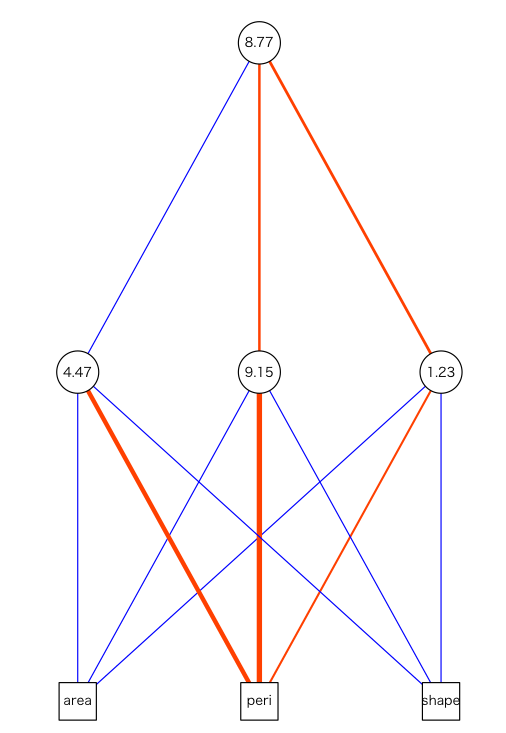
ということでNNやりたいと思ってから一時間くらいでここまでできちゃいましたとさ。

追記

隠れ層の数っていうのがよく分かっていなかったけど、plotしたら分かった。ユニット数と言ったほうがいいのか。

rock.nn <- nnet(log(perm) ~ area + peri + shape, rock1,
                size=5, decay=1e-3, linout=T, skip=T, maxit=1000, Hess=T)
plot.nn(rock.nn)

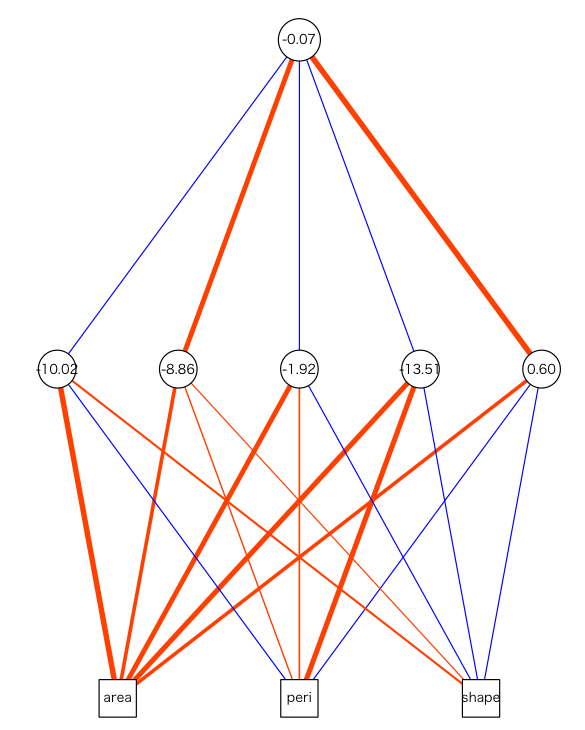
nnetとかをもうちょっと

金先生によるニューラルネットワークの解説
生態学データ解析 - ニューラルネット
CRAN - Package AMORE
- もうちょい複雑なことができるらしい
- 隠れ層の数を2層以上とかにして増やしたい場合はこれがいいのかも
- http://wiki.r-project.org/rwiki/doku.php?id=packages:cran:amore
- AMOEパッケージのドキュメント

最適化とかヘッセ行列がらみの話

wikipedia:ヘッセ行列
東北大の数理計画法の授業のレジメ
- 図が豊富で分かりやすい。上のほうに書いた極小解だが、ヘッセ行列が正定値ではない例もこれで分かる
- 極小解ならば"半"正定値ということなのね。なるほど
http://www.misojiro.t.u-tokyo.ac.jp/~murota/lect-surikeikakuhou/convanalysis031103.pdf
http://www.misojiro.t.u-tokyo.ac.jp/~murota/lect-surikeikakuhou/convopt031103.pdf

*1:上の制約満たさないやつ、ってことかな

*2:ということは交差項とかの作り方の辺も流用できる、ということですね