今日の時系列の授業は時系列というより統計っぽい話。最小二乗法とかからパラメータの分布は自分で一回見てみないとあれだよ、って言われたので調べといた。
説明変数2つくらいのモデルを考える。10000個のデータセットを100個ずつの100個のデータに分ける。それぞれのデータから一つモデルを作り、モデルを計100個作る。それぞれのモデルのパラメータを引っ張ってきて密度トレイスを描いてみた。正規…分布?

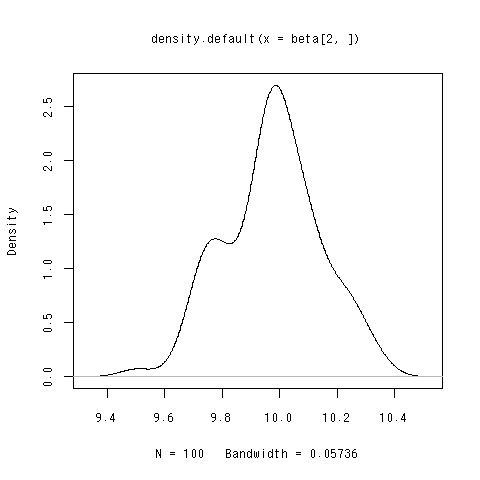
適当すぎる実験コードは下。方法がそもそもこれであっているのがが危ない。てか、for文が遅いのでapplyファミリー走らせないと。。。
#計量時系列分析のやつで遊ぶ #二変数くらいでモデルを考えて、適当に誤差項でばらまく y <- c() n <- 10000 x1 <- c() x2 <- c() rnorm(1) for(i in 1:n){ x1[i] <- rnorm(1)*10 x2[i] <- rnorm(1)*3 y[i] <- 3*x1[i]+10*x2[i]+rnorm(1)*5 } summary(y) x <- cbind(x1,x2) summary(x) beta <- matrix(0,2,100) beta #とりあえずこれで出る solve(t(x)%*%x)%*%t(x)%*%y seq(1,10000,by=100) for(i in seq(1,10000,by=100)){ print(i+1) } 9901+99 y[10000+1] warnings() count <- 1 for(i in seq(1,10000,by=100)){ beta[,count] <- solve(t(x[i:(i+99),])%*%x[i:(i+99),])%*%t(x[i:(i+99),])%*%(y[i:(i+99)]) count <- count+1 } beta hist(beta[1,],nclass=20) hist(beta[2,],nclass=20) png("den1.jpg") plot(density(beta[1,])) dev.off() png("den2.jpg") plot(density(beta[2,])) dev.off() mean(beta[1,]) mean(beta[2,]) var(beta[1,]) var(beta[2,]) 25*solve(t(x)%*%x)