計量時系列分析で習ったことで遊んでみる

正規乱数から相関のあるデータの生成

計量時系列分析で正規乱数から相関のあるデータを生成してみようというやつがあったので、遊んでみる。

平均0、分散1の正規分布に従う乱数(正規乱数)のベクトルを2つ用意。このままでは2つのベクトルは独立なので、無相関。

x<-rnorm(1000)
y<-rnorm(1000)
> cor(x,y)
[1] 0.02898553

そこで以下のように変数変換を施す。
$u=x+\alpha y,v=\alpha x+y$
このような変換を施すと、相関係数 $\frac{2\alpha}{1+\alpha^2}$ を持つようなデータを生成できたことになる。例えば $\alpha=0.7$ とすると、理論値では $\frac{2 \times 0.75}{1+0.75^2}=0.96$ となる。本当になるかを実験してみよう。

a<-0.75
u=x+a*y
v=a*x+y
cor(u,v)
[1] 0.9593697

検定とかはまんどくさなのでやらないけど、大体よさげな感じがしますね。データ解析の時に散々「平均とか相関係数だけ見て、分布とか見ないのは危ない」と言われたので一応散布図を取ってみた。

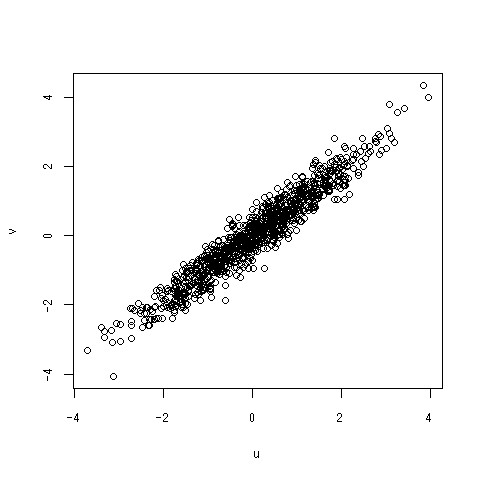
疑った私がバカでした。。。

理論値の求めかた

統計分かってる人には簡単過ぎることだとは思うけど、自分のメモ代わりに残しておくか。なお、最後のほうとか適当に書いてるので、これもとに何かやって失敗しても責任は負いません。とりあえず $X,Y$ は正規乱数と言っているので、 $E[X]=0,E[Y]=0,Var[X]=1,Var[Y]=1$ 。で、このように変換を施す。
$U=X+\alpha Y,V=\alpha X+Y$
次に、 $U$ の平均と分散を求める。
$\begin{eqnarray}E[U]&=&E[X+\alpha Y]\\ &=&E[X]+E[\alpha Y]\\ &=&0+\alpha E[Y]\\ &=&0\\Var[U]&=&E[(U-\bar{U})^2]\\ &=&E[U^2]\\ &=&E[(X+\alpha Y)^2]\\ &=&E[X^2]+2E[\alpha X]+E[\alpha^2]\\ &=&1+2\alpha E[X]+\alpha^2\\ &=&1+\alpha^2 \end{eqnarray}$
$U=X+\alpha Y,V=\alpha X+Y$ についても同様に計算。同様の値が出てくる。次に共分散 $S$ を求める。
$\begin{eqnarray}S[U,V]&=&E[(U-\bar{U})(V-\bar{V})]\\ &=&E[(X+\alpha Y)(\alpha X+Y)]\\ &=&E[\alpha X^2+XY+\alpha^2 XY +\alpha Y^2]\\ &=&E[\alpha X^2]+E[XY]+E[\alpha^2 XY]+E[\alpha Y^2]\\ &=&\alpha E[X^2]+E[X]E[Y]+\alpha E[X]E[Y]+\alpha E[Y^2]\\ &=&2\alpha \end{eqnarray}$
なお、 $E[XY]=E[X]E[Y]$ は[X,Y]が独立という仮定から導いている。

以上より、相関係数を求めると
$\begin{eqnarray}r&=&\frac{S[U,V]}{\sqrt{Var[U]}\sqrt{Var[V]}}\\ &=&\frac{2\alpha}{1+\alpha^2}\end{eqnarray}$
となり、欲しかった相関係数の理論値が計算できた。

この辺の話はここが詳しいかも。

定常時系列データ

ついでにもういっちょ。定常時系列データの作り方も習ったので、Rで生成する関数書いてみた。 $X_t=\beta X_{t-1}+\epsilon_{t}$ で作ってます。

teijyou<-function(b=0.5,n=100){
    x<-rnorm(1)
    for(i in 2:n){
        x[i]<-b*x[i-1]+rnorm(1)
    }
    return(x)
}

定常時系列っぽい感じになってます。

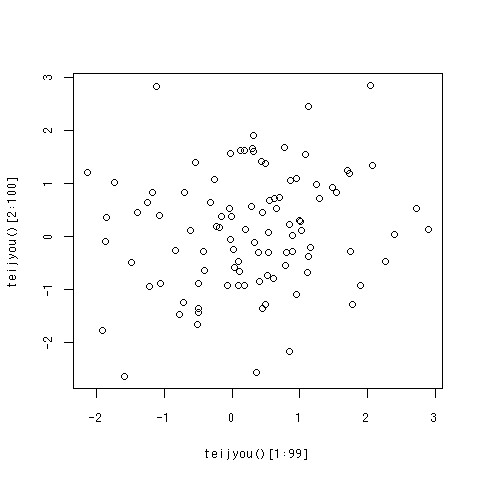
ちなみにこっちで相関係数を出してみたところ、ほぼ0でした。定常時系列データで相関係数0.9とか作れるんでしょうか?