RでK近傍法を用いたクラス分類をするためのコードを書いてみた

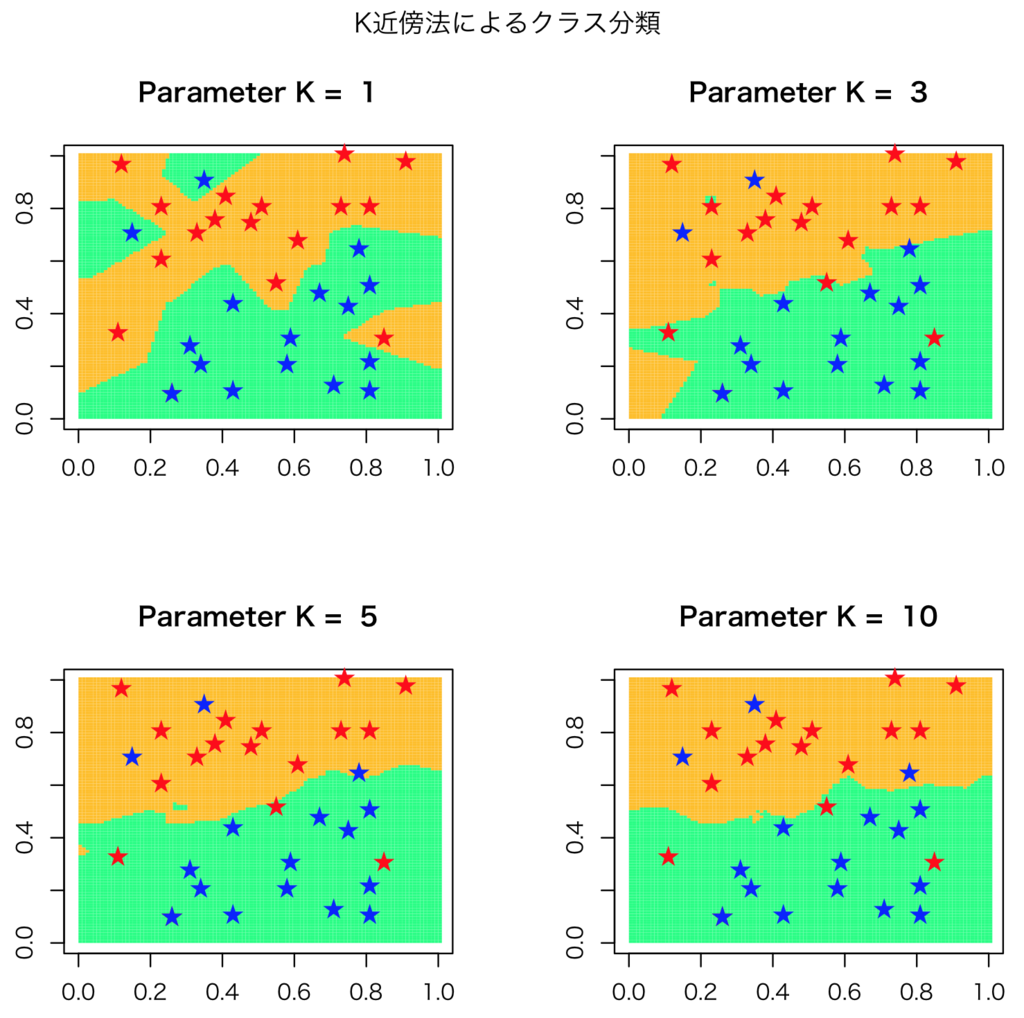
K近傍法による密度推定はいまいちな気がしたので、K近傍法によるクラス分類を行なうことにしました。多クラスでもいいんだけど、まあ2クラスから始めます。クラスに帰属する事後確率が(P123の(2.256式))であることを利用しています。自分で適当にデータ生成して、Kを変えつつ、予測と実際のデータをplotさせてみました。★のマークが実際のデータで、背景の色がついているのが、予測のところです。

d <- "x1,x2,class
0.11,0.33,r
0.59,0.31,b
0.12,0.97,r
0.33,0.71,r
0.38,0.76,r
0.43,0.11,b
0.23,0.61,r
0.48,0.75,r
0.41,0.85,r
0.26,0.10,r
0.23,0.81,r
0.91,0.98,r
0.51,0.81,r
0.73,0.81,r
0.81,0.81,r
0.55,0.52,r
0.61,0.68,r
0.74,1.01,r
0.34,0.21,b
0.58,0.21,b
0.81,0.22,b
0.78,0.65,b
0.75,0.43,b
0.81,0.51,b
0.31,0.28,b
0.81,0.11,b
0.43,0.44,b
0.67,0.48,b
0.26,0.10,b
0.71,0.13,b
0.85,0.31,r
0.35,0.91,b
0.15,0.71,b
"

d <- read.csv(textConnection(d))
plot(d[,c(1,2)],col=ifelse(d$class=="r","red","blue"),pch="★")

prob.c.k.given.x <- function(x,y,k,data){
  x1 <- data$x1;x2 <- data$x2
  o <- rank(mapply(function(X1,X2){sqrt((X1-x)^2 + (X2-y)^2)},x1,x2))
  k.k <- sum(data$class[seq(length(o))[o <= k]] == "r")
  return(k.k / k)
}

knn.classify.with.bayes <- function(k){
  s <- seq(0,1,length.out=100)
  plot(s,s,type="n",main=paste("Parameter K = ",k),xlab="",ylab="")
  for(x in s){
    for(y in s){
      if(prob.c.k.given.x(x+0.005,y+0.005,k,d) > 0.5){
        polygon(c(x,x+0.01,x+0.01,x),c(y,y,y+0.01,y+0.01), xpd=FALSE, col = "#FFBF00", lty=0)
      }else{
        polygon(c(x,x+0.01,x+0.01,x),c(y,y,y+0.01,y+0.01), xpd=FALSE, col = "#00FF80", lty=0)
      }
    }
  }
  points(d[,c(1,2)],col=ifelse(d$class=="r","red","blue"),pch="★")
}

par(oma=c(0,0,2,0))
par(mfrow=c(2,2))
sapply(c(1,3,5,10),knn.classify.with.bayes)
par(xpd=TRUE)
mtext(side=3,outer=TRUE,text="K近傍法によるクラス分類")

P124に書いてある通り、K=1のやつは極限取ると最低でもこれくらいだよ、っていうのが保証されている、ということだけあってか(?)よい感じですね。なんか現実のデータとかを使って分類させてみると面白いかもしれないな。ナダラヤワトソンとかだとhの最適化をしたようにKNNもKの最適化という問題が残っているけど、これはまあ放置することにしよう。

パターン認識と機械学習 上