分散の不均一性とは、xが増えるにつれて、yの分散が大きくなってしまうこと。回帰分析をした結果、説明変数が従属変数をよく説明しているのならば、従属変数の残差の分散は(回帰の仮定より)一定になるはずである。モデルがいいものであるかどうかを判断するためにはこのようなことを調べる必要性がある。
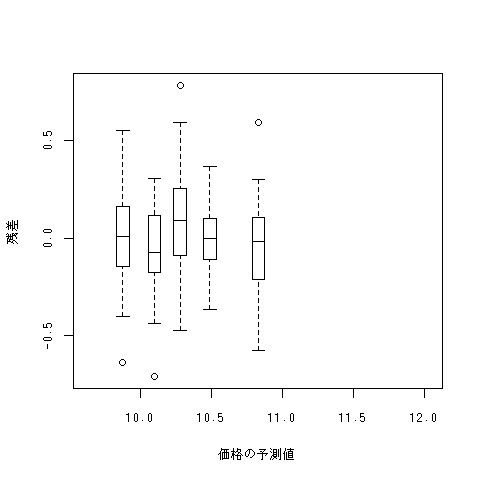
分散の不均一性を調べるためには、授業で使ったplot.strip.n.boxplotsという関数が使える。x軸に従属変数の予測値を、y軸に従属変数の残差を持ってきて、描きたいボックスプロットの数を3番目の引数に持ってくる。これまで習った知識を元にするならば、以下のようなコマンドをやることができる。以下の例では、log.mid.priceをmhw、mid.displacement、is.eu、is.hybridで重回帰している。
plot.strip.n.boxplots(sort(cbind(a,mid.displacement,is.eu,is.hybrid,mhw) %*% lsfit(cbind(mid.displacement,is.eu,is.hybrid,mhw),log.mid.price)$coef),(lsfit(cbind(mid.displacement,is.eu,is.hybrid,mhw),log.mid.price)$residuals),5)
「%*%」はRで行列の積を計算するためのもの。係数と実測値をかけたものの順序統計量をx軸に取り、残差をy軸に取っている*1。
理論的には間違っていないし、統計やら線形代数の勉強をしたのならこのくらいできなとまずいが、データ解析をする上で長いコマンドを打つ疲れる。せめて、行列の積の部分くらい簡単にしたい。ということで、以下のようなことをすれば簡単にできる。
plot.strip.n.boxplots(predict(lm(log.mid.price~mhw+mid.displacement+is.eu+is.hybrid)),lsfit(cbind(mhw,mid.displacement,is.eu,is.hybrid),log.mid.price)$residuals,5)
predictという関数で、予測値を計算することができるそうなので、こっちを使ったほうが楽かもしれない(predictの中に回帰したいもののlmしたやつを投げてやる)。
*1:後述。ソートする必要はなさそうである。やっても間違いではないようだが。